 Home |
Geometria e cielo |
|
Nella geometria della visione, secondo l'Ottica euclidea, si assume che la visione avvenga tramite raggi visivi (non raggi di luce) che partono dall'occhio e toccano la cosa vista. La distanza della cosa dall'occhio non conta conta invece il raggio visivo. Nello stesso modo si postula che la grandezza apparente di un oggetto dipenda solo dall'ampiezza dell'angolo visivo e non dalla reale grandezza dell'oggetto stesso. La seguente animazione, relativa alla visione nel cielo del moto di Marte illustra l'importanza di questa dicotomia tra essere ed apparire e di come si possa tentare, a partire dall'apparire, ricostruire l'essere così come a partire da una scena rappresentata su un quadro riusciamo con la nostra immaginazione a ricostruire l'ambiente reale rappresentato.
|
|
Possiamo però pensare a un secondo modello di tipo diciamo così tolemaico.
|
|
Possiamo concludere che la sola osservazione da Terra del moto di Marte non ci permette di decidere per un modello o per un'altro. Se il
problema è solo quello di prevedere dove si vedrà il pianeta in un dato istante converrà scegliere il modello che rende più
facili i calcoli. Nel modello tolemaico l'orbita presenta una forma strana mentre in quello di Aristarco
le cose sembrano più semplici. 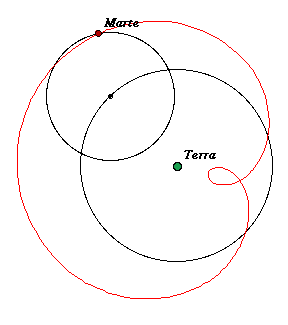
 catastin@mat.uniroma2.it ghione@mat.uniroma2.it |