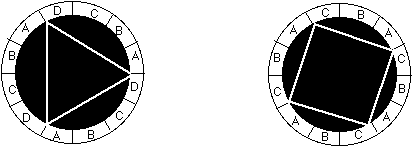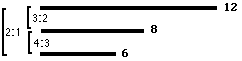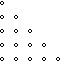|
Premessa
S'io mi trovassi all'estremità dello spazio, ad esempio nel cielo delle stelle fisse, potrei tendere la mano o un bastoncino fuori di quella?
o non potrei?
1
Possiamo provare a immaginare: il vecchio maestro vestito di panni bianchi accompagnava la domanda con silenzi misurati e pazienti e gli
allievi che seguivano le sue argomentazioni sull'infinito nel numero e nello spazio certamente subivano il crescere di una tensione dialettica
che trovava il suo culmine in un gesto: l'alzarsi lentamente in alto del braccio e della bacchetta che teneva in mano. E le argomentazioni,
la domanda, il gesto si fondevano in un'unica immagine, piena di significati e di poesia, che ben esprimeva l'essere filosofo, come chiedeva
di essere chiamato Pitagora, cioè amante della sapienza.
Il maestro di cui parla Eudemo nella citazione appena presentata è Archita, uno dei più autorevoli esponenti della scuola pitagorica.
Intendiamo qui affrontare alcuni aspetti del pensiero di Pitagora e della sua scuola presentando punti di vista diversi da quelli tradizionali
non tanto per proporre una nuova interpretazione che pretenda di essere piu' veritiera e documentata delle altre, quanto piuttosto per le
suggestioni che da quel pensiero ci vengono. Siamo infatti convinti che alcuni nodi che tengono unito non solo il pensiero matematico ma
anche quello piu' strettamente filosofico si possano ritrovare, nella loro originaria pregnanza comunicativa, nella scuola dei pitagorici che,
per primi, diffusero i semi della nostra cultura scientifica in quella regione che aveva avuto il nome di Italia, cioè la Calabria.
Raccogliere oggi alcuni di quei semi alla luce di una interpretazione diversa da quella tradizionale aristotelica, ci da' una forza in piu',
come una gioia, che deriva dalla consapevolezza che le nostre radici sono ancora vitali. Attingendo ad esse puo' essere forse piu' facile
contrapporsi al tentativo di sgretolare la cultura, le discipline e, all'interno di queste, i risultati riducendoli a frammenti di un vaso
spezzato di cui non se ne riconosce piu' la forma globale, teorica, astratta, il senso, insomma, il senso complessivo.
Esiste un tipo particolare di produttività creativa del pensiero che si esprime con rigore nel pensiero scientifico. Essa consiste nel
dare vita a un ordine tra elementi diversi, in modo da far emergere relazioni che prima non erano presenti o non erano evidenti, raggruppamenti
originali, connessioni nuove. Ciò che si ottiene alla fine è la presenza nei dati iniziali di una nuova struttura, ottenuta con operazioni
che precedono le concettualizzazioni logiche e che si avvalgono, tra l'altro, di procedimenti metaforici e di analogie.
La metafora non è solo uno strumento proprio dell'espressione poetica, una semplice questione di felice scelta di parole, ma un
meccanismo di trasposizione di significati da un terreno conosciuto a un ambito nuovo che, attraverso l'analogia, trova una sua struttura.
La metafora è un motore potente che muove il pensiero: il nostro sistema concettuale è fondato su basi essenzialmente metaforiche,
che intervengono in modo continuo nella struttura delle percezioni e delle idee.
La potenza della metafora ha però un limite: la mancanza di rigore logico. Una civiltà che non sappia affiancare all'aspetto creativo e
analogico del suo pensiero la verifica dell'affidabiltà delle affermazioni prodotte, non potrà mai avere uno sviluppo scientifico.
Due importanti fattori oggi nella nostra scuola, contribuiscono alla mortificazione, in campo scientifico, delle capacità "creative"degli
studenti. Si trascura da una parte l'affinamento di tecniche logiche di pensiero che non sono affatto patrimonio spontaneo della mente
2
(le regole di inferenza
3
, ad esempio, e i fondamenti della logica formale) e che quindi vanno adeguatamente educate, e dall'altra si
sottopongono gli alunni a dosi massicce di argomenti impegnativi spiegati tramite immagini, analogie, comparazioni anche suggestive che
mostrano somiglianze ma non dimostrano nulla. In questo modo non si formano nella loro mente modelli o capacità scientifiche, e
neanche semplici informazioni, ma piuttosto immagini di una scienza ermetica e sostanzialmente irrazionale. Il risultato finale di
questo quadro è che non viene educato nè l'aspetto logico né quello metaforico del pensiero, togliendo così forza e
incisività alla sua azione e relegando una gran quantità di studenti nella schiera di coloro che mancano di autonomia
ideativa e di immaginazione.
Riteniamo che a volte l'allontanarsi da prospettive troppo vicine ai problemi da affrontare aiuti a raggiungere una soddisfacente chiarezza.
Riflettere sugli sforzi speculativi dei filosofi della scuola dei pitagorici può aiutarci anche a tener nel giusto conto e nel giusto equilibrio,
nell'educazione del pensiero di oggi, l'irrinunciabile obiettivo della padronanza dei linguaggi verbali e delle forme simboliche e l'esigenza
altrettanto forte della mente di usare l'immagine come strumento di comprensione. Thom ci avverte
4
:
[...] dubito che...in un universo in cui tutti i fenomeni fossero retti da uno schema matematicamente coerente, ma privo di contenuto
traducibile in immagini, la mente umana sarebbe pienamente soddisfatta...Privato di ogni possibilità intellettiva cioè di
interpretazione geometrica dello schema dato, l'uomo cercherà di crearsi nonostante tutto una giustificazione intuitiva dello
schema dato attraverso immagini appropriate oppure sprofonderà in una rassegnata incomprensione che l'abitudine trasformerà
in indifferenza.
Dal mito al numero
La scuola pitagorica, dando per la prima volta alla matematica, all'aritmetica e alla geometria, la dignita' di un'arte speculativa, che si
fonda su teoremi chiaramente enunciati e su conseguenti dimostrazioni generali, fornisce i primi modelli astratti, che noi diciamo
pre-scientifici, con i quali far corrispondere i fatti della natura con enti teorici alla base del modello.
La caratteristica di questi modelli è quella di aggiungere alle descrizioni qualitative di fenomeni naturali complessi, che erano
le sole all'epoca esistenti, una descrizione anche quantitativa. Ciò renderà possibile il passaggio dalle analogie della mitologia,
prevalentemente cosmogoniche e basate solo su somiglianze
5
, a quelle pitagoriche, fondate sul concetto di rapporto, che permetteranno l'avvio di una nuova forma di interpretazione razionale della
realtà sulla base di modelli matematici. La natura dell'Unverso, dunque, esprimibile attraverso i rapporti, e' simile a quella della
mente che la contempla. Il logoV (rapporto ma anche argomentazione razionale)
è per la scuola di Pitagora il fondamento per la comprensione del mondo
6
:
I Pitagorici affermano che [criterio di verità] sia il logoV ,
non inteso nel significato generale, ma in quello che deriva dalle scienze matematiche-come appunto diceva Filolao- e che, essendo legato
alla percezione mentale della natura del tutto, abbia con essa una certa affinità, se è vero come è vero, che
il simile viene compreso naturalmente dal simile.
L'uso dello stesso termine, logos, per indicare rapporto in senso matematico e argomentazione razionale è molto suggestivo e porta ad
aggiungere profondità e spessore al pensiero pitagorico. Il rapporto A:B sembra essere visto come un movimento di pensiero, una qualche
costruzione rigorosa, quantitativa che lega A a B, che permette di dedurre B da A come una qualunque altra forma di ragionamento.
L'argomentare non è sempre esplicitato, anzi il più delle volte l'individuazione di una unità che misuri esattamente
le due realtà A e B è implicita e racchiusa nei simboli numerici propri del rapporto. Il rapporto 2:3 non è
il numero 0,6666.... ma l'abbreviazione della seguente argomentazione: se tra un A e un B esiste tale rapporto, allora B è tre
volte la metà di A o sei volte un quarto di A o15 volte un decimo di A ecc.
Il costituirsi di un rapporto pemette di dare alla descrizione delle entita' in gioco un valore di "verità" pari a quello che
il ragionare astratto avrebbe raggiunto, con Aristotele, attraverso sillogismi ben formati. L'identità del termine, tra rapporto e
ragione, toglie dunque al rapporto il solo connotato numerico e gli conferisce la dignità di pensiero, di un pensiero che si muove
e porta a individuare forme, somiglianze, leggi, principi universali.
Siamo d'accordo con Cardini
7
quando sostiene che la scuola pitagorica ha prodotto un movimento di pensiero organizzato, complesso,
con una storia e una tradizione dietro di se', ricco di un'intima forza speculativa, orientato verso vari aspetti dell'attività
della mente, con sue proprie dottrine, con una sua concezione dell'universo fondata su principi teorici, ma non tanto dogmatica da
tramandarsi immobile, anzi ricca di problemi e disposta a coraggiosi adeguamenti alla realtà di volta in volta intuita.
Questo organismo non era ne' di puri iniziati di una setta religiosa ne' di seguaci di una dottrina politica. La capacita' di adeguarsi
e di operare cambiamenti toglie al movimento, a nostro parere, la prevalenza della connotazione mistica. Costoro si qualificavano con
un nome di scuola "i Pitagorici" esprimente insieme un genere di vita quanto mai parco e severo e una dottrina di alto e originale valore
speculativo. Il pentagramma, che racchiude il segreto della sezione aurea e dell'incommensurabilità pare fosse anche il simbolo di
riconoscimento della fraternità che univa gli adepti.
Tutto è numero?
Il concetto di monade e di numero nella scuola pitagorica ci pare molto impoverito nel modo in cui è riportato nei principali testi
di storia della scienza
8
:
Col termine "numeri" i pitagorici intendevano soltanto i numeri interi, concepiti come le collezioni di piu' unita'. Non fecero particolari
indagini sulla natura di queste unita', limitandosi a rappresentarle come punti, circondati ciascuno da uno spazio vuoto. Proprio questa
rappresentazione spaziale facilito' il passaggio, caratteristicamente arcaico, dalla concezione del numero come "chiave" e rapporto
alla sua concezione come costituente fisico elementare delle cose.
oppure
9
:
Il punto, elemento unitario delle cose, se da una parte conduceva alla loro rappresentazione geometrica, dall'altra era concepito come
un corpicciolo, unità materiale o monade. Or dunque la formula paradossale ┤le cose sono numeri¬ viene a dire che ogni materia è
composta di elementi o punto materiali, di piccola ma non nulla grandezza, e che dalla figurazione ˝ numero e ordine ˝ di codesti punti,
fra loro identici e qualitativamente indifferenti, dipendono tutte le proprietà e differenze apparenti dei corpi.
o ancora, in un testo di storia della filosofia per scuola media superiore
10
:
L'unità aritmetica era associata al punto geometrico e questo non era concepito come inesteso, ma al contrario come un
"sassolino" ...Una forma geometrica era pertanto descrivibile come il risultato della disposizione di un certo numero di unità
secondo uno schema; questa identificazione di geometria e matematica si rifletteva nella distinzione di numeri quadrati, rettangolari,
oblunghi o assimilabili ad altre figure geometriche.
Questa impostazione porta a pensare che l'identificazione tra il numero e il mondo si risolvesse in gran parte, per i pitagorici,
con una corrispondenza tra la figurazione o la quantità di punti materiali (monadi) che compongono ogni corpo e le proprietà
apparenti di questi ultimi.
L'idea che se ne ricava è quella di un pensiero pitagorico ingenuo e relativamente primitivo, legato al numero dalla "numerologiaì,
forma di interpretazione della realtà impregnata di magia e di superstizione, con l'aggiunta, nel corpo della dottrina, di ipotesi che
risultano, proprio perchè primitive, incomprensibili e forzate.
Gran parte delle difficoltà e delle mistificazioni che si presentano oggi dipendono dalla scarsa familiarità che abbiamo con i modi
di pensiero pre-logici, che, proprio per questa ragione, acquistano particolare valore nell'esplorazione di tutti gli strumenti conoscitivi
del pensiero, anche quelli che, con l'evolversi del tempo e delle conoscenze, sono rimasti in ombra, oscurati dallo splendore e
dall'incisività della logica aristotelica. Il lavoro di Aristotele infatti ha delegittimato e come tagliato fuori un settore di
pensiero, quello appunto pre-scientifico, profondamente fecondo e produttivo, che ha posto comunque per la prima volta l'esigenza di una
metodologia di pensiero rigorosa e ha portato progressivamente a un affinamento delle tecniche argomentative.
Il problema che qui vogliamo affrontare non semplicemente quello di padroneggiare idee diverse, che differiscono dalle nostre, bensì
quello scoprire e di tenere in dovuto conto differenze nelle premesse fondamentali del pensiero e nei veri e propri metodi del pensare,
differenze che se trascurate tendono a rendere le nostre interpretazioni della filosofia pitagorica (presocratica in genere) una proiezione,
nella terminologia dell'epoca, di contenuti tipicamente moderni.
Può forse consolarci il fatto che anche per Aristotele, molto più vicino ai Pitagorici di noi, fosse difficile entrare
pienamente in sintonia con certe loro affermazioni. Ci racconta ad esempio Alessandro di Afrodisia
11
:
Assumendo infatti che il carattere distintivo della giustizia sia la reciprocita' e l'uguaglianza, [e] riscontrato questa caartteristica nei
numeri, [i Pitagorici] dicevano per questo motivo che la giustizia foss il primo numero del tipo "uguale per uguale"
12
:
infatti [ritenevano] che una definizione si applichi sopratutto alla prima di ciascuna delle cose aventi la stessa definizione.
Bisogna tener presente che per i pitagorici il primo, nella serie numerica, dei numeri che esprimeva i rapporti presenti in una determinata
cosa, ne era chiamato il "principio primo"e diventava il veicolo di una metafora che esprimeva l'essenza della cosa stessa e che permetteva
loro di affermare che
13
:
Ed in effetti tutte le cose conosciute hanno numero: non ci e' infatti possibile, senza di esso, pensare ne' conoscere niente.
Essi trovavano così una corrispondenza, tra la struttura del "quattro", del primo quadrato, e la struttura intima della giustizia,
articolata nel modo seguente: il quattro sta alle sue due parti uguali che comunque combinate tra loro (per somma o per prodotto) lo
riproducono, come la giustizia sta alle sue due parti uguali, quanto si è avuto e quanto si è contraccacambiato, che ne
costituiscono la sostanza.
Aristotele rifiuta nettamente questa corrispondenza e con essa il metodo in generale
14
:
Fu dunque Pitagora il primo a trattare della virtù, ma non nel modo corretto; in effetti, riducendo le virtu' ai numeri non
ne costruiva la teoria loro propria: infatti la giustizia non e' un numero "uguale per uguale"
Il modo corretto a cui pensava Aristotele era quello delle norme della logica, norme che non potevano accettare che il concetto di virtù
potesse essere ricondotto a un numero. In effetti con Aristotele la logica diventa un parametro potente e indiscutibile con cui giudicare
qualunque tipo di affermazioni, da quelle comuni a quelle scientifiche o filosofiche.
La monade e l'immagine
Attraverso la lettura dei pochi frammenti, più o meno dubbi, che ci restano dei Pitagorici, si evidenziano due movimenti di fondo del
loro pensiero: l'uso dell'immagine come veicolo di una metafora che permetta di trasferire strutture, e la continua ricerca dell'unificazione
di dati molteplici in un solo insieme coerente e strutturato. Questi due movimenti sono un meccanismo stabile della mente per la produzione di
conoscenza, e li ritroviamo immutati nel tempo anche oggi. Quello che è cambiato sono ovviamenti gli strumenti culturali che il nostro
pensiero ha a disposizione per queste operazioni. Noi oggi per esempio siamo sommersi da informazioni date attraverso forme simboliche di
scrittura o tramite immagini artificiali, costruite appositamente per l'informazione stessa. Immagini, come quelle scientifiche, già
strutturate, esplicative, descrittive.
Al tempo dei Pitagorici invece le immagini a disposizione erano prevalentemente quelle offerte dalla natura, scenari naturali in cui la
struttura a volte si imponeva, a volte andava individuata con intelligenza:
Ora, esiste forse spettacolo più bello di quello del giorno? Poi viene lo spettacolo della notte che, da parte sua, offre tutt'altra
visione. E siccome il cielo nel suo ciclico rinnovarsi non cessa di far seguire infinite notti a infiniti giorni, non smette neppure di
mostrare agli uomini l'uno e il due, finchè anche l'uomo più tardo non apprenda i rudimenti del calcolo; e del resto, anche
il tre e il quattro e molti altri numeri ciascuno di noi può apprenderli dall'osservazione di questi fenomeni. Ma di questa pluralità
Dio fece un'unità allorchè creò la luna, la quale, talvolta diminuendo, tal altra aumentando le sue dimensioni, traccia,
finchè è visibile, un altro tipo di giorno, che dura quindici giorni e altrettante notti. E questo moto di rivoluzione, se si
ha l'accortezza di fare un'unità del suo intero ciclo, oserei dire che è tale da essere compreso anche dal meno intelligente
dei viventi, a cui dio abbia fatto dono della naturale capacità di apprendere.
Epinomide enuncia con leggerezza una legge molto importante: quando di un fenomeno complesso si riesce a fare un'unità, allora
la comprensione del fenomeno stesso risulta facile "anche al meno intelligente dei viventi
15
.
La costruzione di questa unità porta a usare inizialmente in maniera privilegiata gli aspetti di pensiero legati a processi gestaltici,
di sintesi, da esplicare, nel difetto di leggi logiche rigorose, in enunciazioni create dall'analogia. Troviamo in Aetio un esempio di
ragionamento imperfetto, attribuito a Filolao, che per via analogica stabilisce un rapporto tra la grandezza degli animali sulla terra e sulla
luna e la durata dei giorni lunari quindici volte più lunghi di quelli terrestri
16
:
Alcuni Pitagorici, fra cui Filolao, dicono che la luna è costituita di terra , per il fatto che è abitata da animali e da piante
come la nostra terra; sono però più grandi e più belli; dicono infatti che gli animali che si trovano su di essa sono
quindici volte più grandi e non espellono escrementi e che il giorno è altrettante volte più lungo.
Attraverso l'analogia la forma e il significato individuati nell'osservazione del mondo sensibile si spostavano da un dominio all'altro,
strutturando e dando significati unitari. Questo è il senso profondo che acquista la necessità, l'importanza, anche per i
Pitagorici, del movimento di pensiero rivolto alla continua ricerca della monade, dell'uno: l'uno è il risultato dell'individuazione
in un molteplice slegato e frammentario, senza quindi alcun valore conoscitivo, di una struttura significativa e significante, che conferisce
identità unica al molteplice, e che diventa patrimonio del pensiero alla pari di un concetto.
Troviamo in Giamblico
17
:
I Pitagorici chiamavano l'1 "intelligenza " perchè pensavano che questa è simile all'Uno [...] Lo chiamavano anche [...] "modello",
"ordine"...
E ancora ci dice, sempre riferendosi ai Pitagorici
18
:
Esso (l'uno) è di fatto forma delle forme, come creazione per il suo potere creativo e intellezione per il suo potere intellettivo[...]
Come senza l'1 nessuna cosa può assolutamente costituirsi, così senza di esso non ci può essere neppure un qualsiasi atto
conoscitivo, come fosse la pura luce, [...] soprattutto perchè l'1 ha il potere di conciliare e combinare insieme le cose fatte di
molteplice mescolanza, sia le cose assolutamente differenti tra loro, proprio come fa Dio col suo potere di ricavare da elementi altrettanto
opposti l'armonia e l'unità di questo mondo.
L'uno, la monade
19
è dunque intesa come unita' strutturata, come un raggruppamento in un unico di una molteplicità che diventa nuovo strumento di
misura. In questo modo alla visione di monade come atomo si può sovrapporre quella di una gerarchia di unità che esprimono
complessità crescente. Si osservi ad esempio come in questa testimonianza di Proclo sulla visione astronomico-geometrica del cosmo
dei Pitagorici si possano individuare gerarchie di tal genere, che si mescolano a considerazioni analogiche
20
:
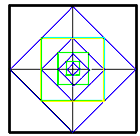
Bisogna non dimenticare che Filolao dedico' l'angolo del triangoloa quattro divinita', quello del quadrato a tre, per mostrare la loro
compenetrazione reciproca e la compartecipazione di tutte le cose in tutte le cose, dei dispari nei pari e dei pari nei dispari. Quindi,
la triade tetradica e la tetrade triadica, partecipando delle cose buone feconde e produttrici, tengono insieme l'ordinamento complessivo
delle cose generate. La dozzina, risultante da esse, estende il potere di Zeus ad una sola unita'. Filolao afferma infatti che l'angolo del
dodecagono pertiene a Zeus, in quanto Zeus comprende in un'unica combinazione l'intero numero della dozzina.
In questo passo il triangolo equilatero, il quadrato e il dodecagono, ciascuno con una propria perfezione e quindi adatti a misurare cose divine,
strutturano il cerchio delle 12 costellazioni dello Zodiaco, che creano a loro volta nel tempo una monade, l'anno, e occupano per questo
una posizione di privilegio rispetto alle altre stelle.
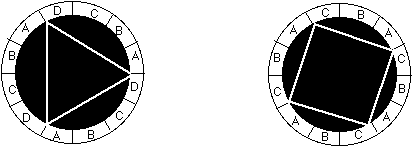
Così a quattro divinità viene consacrato l'angolo del triangolo, e a tre quello del quadrato. E al dio più importante,
Giove, è dedicato l'angolo del dodecagono, perchè contribuisce a riunire in un'unica configurazione tutte le monadi, dalla più
semplice alla più complessa. Il dodecagono infatti divide lo zodiaco nelle singole costellazioni (l'unità più semplice) e
Giove
21
, con la sua orbita che percorre lo Zodiaco in 12 anni, abbraccia in un tutto unico l'intero numero del dodici, costruendo la monade
principale, che contiene tutte le altre: l'1 dato da ogni costellazione, e la triade e la tetrade compenetrate nelle successive ripartizioni.
Nel pensiero pitagorico cio' che principalmente struttura una monade e' il rapporto aritmetico, e per questo essa ha una natura matematica che
trasmette a tutto il cosmo. Strutture articolate che vengono descritte da piu' rapporti, come la cetra, o i movimenti degli astri, che per i
Pitagorici producevano suoni
22
, trovano il loro elemento strutturante in un "divisore comune" che consente di esprimere in modo unitario
tutti i rapporti che intervengono ed è calcolabile coll'"algoritmo euclideo" delle divisioni successive di origine antichissima.
Supponiamo ad esempio di avere quattro corde e di voler assegnare ad ognuna una lunghezza in modo che, prendendole a coppie, una sia
lunga la metà dell'altra, una misuri due l'altra tre, una misuri tre l'altra 4. E' ovvio che si impone di trovare una misura comune
che soddisfi le condizioni poste. La corda più lunga verrà divisa in dodicesimi che serviranno a misurare le altre. La prima,
che deve esserne la metà sarà così sei dodicesimi (1: 2), la seconda otto dodicesimi (2 : 3), la terza nove dodicesimi
(3 : 4).
La struttura realizzata riproduce i rapporti di ottava, quinta e quarta, basi dell'armonia musicale, e non cambia se la lunghezza
delle corde è espressa in 6, 8, 9, 12 metri, braccia, centimetri...
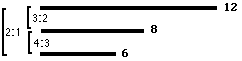
Vengono in ogni caso prodotti oggetti tutti equivalenti tra loro, e si crea una nuova monade che potremmo chiamare "lira a tre corde".
Che a questa stessa lira si possano per via analogica o addirittura quantitativa rapportare altre cose - un'organo, per esempio, o una
configurazione armonica di un qualche movimento celeste - e', crediamo, una novita' importante del pensiero pitagorico.
La monade può essere allora estremamente complessa, come complesso e' individuare in un qualche molteplice una struttura ed e' questa,
come lo stesso Leibniz, aveva osservato che agisce direttamente sul pensiero
23
:
Lo stato passeggero che racchiude e rappresenta una moltitudine nell'unità o nella sostanza semplice [che per Lebiniz e' la monade]
, altro non e' che cio' che si chiama percezione.
L'idea che la monade non possa essere ridotta a punti materiali estesi ed uguali tra loro ma piuttosto vada vista come una unità
strutturata confacentesi alla natura del pensiero e a ciò che essa modellizza, ci sembra possa essere un'idea già chiaramente presente nella
scuola
ptagorica.
I sassolini
Dice Teofrasto
24
Questo infatti e' proprio di chi e' maturo ed assennato, come Archita racontava una volta che facese Eurito quando disponeva certi sassolini:
egli diceva infatti che questo era il numero che toccava all'uomo, quello al cavallo, quello ad una qualche altra cosa
Aristotele in effetti nel De caelo interpreta il numero dei Pitagorici alla stregua di un sassolino, pur se immateriale
25
:
La medesima cosa accade a quelli che vogliono il cielo composto di numeri. C'e' infatti chi dice, come alcuni pitagorici, che la natura e'
composta di numeri. Ora e' evidente che i corpi fisici hanno peso e leggerezza, e che le unita' non possono unendosi, dar origine ad un corpo,
ne' avere peso.
e sembra non capire
26
:
Ma neppure è stato definito come i numeri siano causa delle sostanze e dell'essere, se come limiti, al modo che i punti sono limiti delle
grandezze, e cioè al modo seguito da Eurito: quando, dicendo che ciascun numero è causa di ciascuna cosa, questo numero dell'uomo
e quello del cavallo, disponeva i suoi sassolini in modo da ottenere, così come quelli che ottengono dai numeri le figure del triangolo
e del quadrato, le figure [degli animali e] delle piante.
Ma Alessandro di Afrodisia
27
spiega meglio e ci racconta che per Eurito, 250 era il numero dell'uomo e 360 quello della pianta - il che gia' dice che la pianta e' poco piu'
di una volta e mezzo l'uomo - e che i sassolini che lui usava erano piu o meno uguali nella forma ma di diverso colore. In realta' cio'
che Eurito cercava di realizzare col suo mosaico era un modello, una immagine strutturata dell'uomo che potesse essere memorizzata come
un concetto
28
, ma che a differenza del concetto, potesse anche mostrare i vari rapporti tra le parti del corpo in termini di numero di
sassolini (l'uno che che struttura): ad esempio di 50 pietruzze e' l'altezza di tutto l'uomo, mentre il viso e' di 10 e 30 le braccia.
Nasce cosi' una nuova monade, una nuova unita' piu' complessa, ma in un certo senso stabile, che e' l'immagine dell'uomo con le sue
proporzioni, base per nuovi esercizi di pensiero. L'uomo e l'armonia delle sue forme era un tema caro alla sensibilità greca,
ripreso, come è noto, dagli studi rinascimentali sulle proporzioni del corpo umano e in generale sulla teoria delle proporzioni
29
.
Galeno riporta che
30
:
C'è una rinomata statua di Policleto che è chiamata Canone appunto perchè presenta la perfetta proporzione di tutte le parti
tra di loro.
e ancora
31
:
[...] ...la bellezza egli [Crisppo] ritiene che consista nella proporzione non degli elementi , ma delle parti, cioè di un dito
riapetto a un altro dito, di tutte le dita rispetto al metacarpo e al carpo, di queste rispetto all'avambraccio, dell'avambraccio rispetto
al braccio e infine di tutte le parti fra loro, come è scritto nel Canone di Policleto. Il quale Policleto, dopo aver esposto in questo
suo scritto tutte le proporzione del corpo, convalidò la sua teoria con un'opera, costruendo una statua secondo i precetti da lui esposti
e la chiamò con lo stesso nome dello scritto, Canone.
Il sassolino allora diventa una metafora, un'immagine che ci ricorda che l'aritmetica ha necessariamente una natura discreta, contrapposta al
continuo geometrico. Ma la disposizione di unità in una figurazione può, come abbiamo visto, indurre abbastanza facilmente a
considerazioni errate
32
:
Una forma geometrica era pertanto descrivibile come il risultato della disposizione di un certo numero di unità secondo uno schema.
Il numero triangolare non descrive il triangolo come ente geometrico: se calcolo il semiprodotto della base per l'altezza (l'area del triangolo)
non ottengo il numero di punti che costituiscono il triangolo stesso. E' il numero triangolare che viene descritto come disposizione di un
certo numero di unità secondo una forma geometrica, non il contrario. Quello che la figurazione del numero crea è una struttura
che permette di arrivare a esprimere considerazioni o compiere determinate operazioni, che altrimenti sarebbero complicate. Così cio'
che oggi scriveremo come " 1 + 2 + 3 + 4 + ...." viene rappresentato come un triangolo
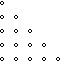
che ne traduce, attraverso la sua forma visiva geometrica, non solo una struttura facilmente memorizzabile, ma anche una sorta di principio
generatore di pensiero (l'aggiunta di righe successive, ognuna con un elemento in più di quella precedente) ben piu' significativo
dei nostri puntini. La forma poi permette altre operazioni34 : accostando per esempio tra loro due di tali unita' strutturate
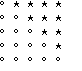
appare un rettangolo col quale nasce, nel nostro pensiero, una "dimostrazione" della formula che oggi scriveremmo
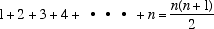
la quale e' dimostrazione (non induttiva, non logicamente formalizzata) proprio perche' il principio generatore, che consiste nell'aggiungere
una riga di pallini e una colonna di asterischi, si riproduce simile a se stesso indefinitamente.
Un ulteriore esempio di questa natura si trova, a chiusura dell'articolo, nella nostra ricostruzione fantastica e scherzosa di un dialogo
tra due Pitagorici, Brontino e Deonono, nel quale si ipotizza la "dimostrazione" dell'irrazionalità della diagonale del quadrato.
L'analogia
Esiste un legame profondo e in un certo senso insospettato tra il concetto di monade cosi' come lo intendiamo e l'analogia. Archimede
nell'Arenario , con lo scopo di trovare un nome a grandi numeri e di eseguire calcoli con essi, usa il metodo seguente: partendo dall'unita'
si assegna un nome ai primi 10.000 numeri: si dice che sono una miriade. Con la miriade possiamo costruire una miriade e dieci, una miriade e
100, una miriade e 1000 , 2 miriadi ecc. e, proseguendo in questo modo, arrivare alla miriade di miriadi e dare cosi' un nome a ogni numero da
1 a 108. A questo punto, per analogia, Archimede pensa alla miriade di miriade come a una nuova unita' (monaV)35 , una monade alla quale da'
il nome di "unita' dei numeri di tipo 2" . Di queste unita' se ne possono fare ancora una miriade di miriadi arrivando in questo modo, ad
avere un nome per tutti i numeri fino a 1016.E la miriade di miriadi di unita' dei numeri di tipo 2 diventa ancora uno, diventa' "unita' dei
numeri di tipo 3" e cosi' via.
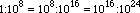
Il processo continuo di riduzione all'uno e' palese e la natura strutturante della monade esplicita. Potremmo esprimere in forma concisa,
come e' costume dei matematici, in una formula questo concetto:
1 : A = A : B
Ecco che appare l'uno a primo membro che misura la moltitudine A, la quale poi, per analogia diventa essa stessa come l'uno, nuova monade con
cui misurare la moltitudine B. E' interessante notare come il termine tecnico usato all epoca per definire la proporzione continua
(tra tre termini A : B = B : C) sia "analogia" (analogia): il rapporto tra A e B è analogo al rapporto tra B e C.
Il metodo analogico, antichissimo, trova nella proporzione aritmetica una sua prima formalizzazione rigorosa che produce anche un termine
che diventerà poi, nel linguaggio comune, sinonimo di una forma generale di pensiero pervasivo nelle arti come nelle scienze. Ma e'
nelle scienze soprattutto che il metodo analogico ha prodotto i maggiori risultati. Un modello scientifico, fornisce, in un certo senso,
una corrispondenza analogica tra gli elementi strutturati di un oggetto teorico essenzialmente matematico, e gli elementi fisici che con
quel modello si vuol rappresentare. Seguiamo su un esempio di natura astronomica come l'analogia si sia sviluppata, dai pitagorici, ad
Aristarco di Samo ad Archimede.
Aristotele dice nel De coelo
35
:
I più dicono che la terra sta nel centro...il contrario affermano i filosofi Italici, chamati Pitagorici; essi dicono che nel mezzo
c'è fuoco, e che la terra è un astro, che movendosi in circolo intorno al centro produce la notte ed il giorno. E inoltre
suppongono un'altra terra opposta a questa, che chiamano antiterra. Essi non indagano le ragioni e la cause partendo dai fenomeni, ma
al contrario, cercano di tirare i fenomeni a certe loro ragioni e opinioni, e a queste adattarli. Ed anche molti altri sarebbero
d'accordo con loro che non se debba assegnare alla terra la sede nel centro, qualora ricavassero le proprie convinzioni non dall'osservazione
dei fenomeni , ma piuttosto da astratti ragionamenti . Quelli infatti ritengono che al corpo più nobile convenga il luogo più
nobile; che il fuoco è più nobile della terra; che i termini valgono più delle parti intermedie; e termini sono tanto
la parte estrema che il centro. Sicchè per analogia con queste loro affermazioni, non la terra essi credono che occupi il centro della
sfera, ma il fuoco.
Dunque Aristotele attribuisce ai Pitagorici il tentativo di formulare modelli scientifici fondati su "astratti ragionamenti" centrati sul
metodo analogico: il rapporto tra il fuoco e la terra, il primo più nobile del secondo, è analogo a quello tra il centro e
l'universo intero e per questo e' il fuoco che sta al centro.Questa analogia viene ripresa da Aristarco di Samo, il fondatore della teoria
eliocentrica, il quale riconsidera il rapporto tra il centro e l'universo per determinare quantitativamente la dimensione dell'universo stesso
secondo quanto ci riferisce Archimede, sempre nell'Arenario
36
:
Lui [Aristarco] suppone che le stelle fisse e il sole restino immobili, che la terra giri attorno al sole su una circonferenza che ha il
suo centro nel sole e che la sfera delle stelle fisse che si estende attorno allo stesso centro, cioe' al sole, abbia una grandezza tale che il
rapporto del cerchio , sul quale si suppone che giri la terra, con la distanza delle stelle fisse e' analogo al rapporto del centro della sfera
con la sua superficie. Certo questo e' evidentemente impossibile dal momento che il centro della sfera non ha grandezza e quindi non puo' avere
rapporto (logon) con la superficie della sfera. Ma si puo' credere che il ragionamento di Aristarco sia il seguente: poiche' ammettiamo che la
terra e' in un qualche modo il centro del mondo, il rapporto tra la terra e quello che noi chiamiamo comunemente il mondo (il mondo e' la
sfera con centro la terra e raggio la distanza terra-sole) e' uguale al rapportodella sfera che contiene il cerchio su cui si muove la terra
con la sfera delle stelle fisse.
La conclusione dunque alla quale arriva Archimede e' che il rapporto tra la grandezza della terra e quello del mondo e' uguale al rapporto
tra la grandezza del mondo e quella dell'universo. Ancora una proporzione di tre termini in cui la terra nasce come unita' di misura del mondo
il quale poi diventa l'uno, la monade, il "punto" al centro dell'universo. Questa analogia, ovviamente, conoscendo la grandezza della terra e
quella del mondo cioe' la distanza terra-sole, consente di calcolare la grandezza di questo universo ipotizzato da Aristarco. La forza
dell'analogia come metodo quantitativo, al di la' dell'esattezza dei modelli elaborati, apre la via al nascere di una scienza esatta, fondata
su modelli teorici e "ragionamenti astratti" che trovera' pieno sviluppo in ogni campo a partire dal III secolo a.C.
In altre parti lo stesso Aristotele sembra apprezzare molto il metodo analogico come strumento di pensiero
37
:
[...] ma e' grandissimo veramente che ci sia l'espressione metaforica. Solo questa non si puo' mutuare da altri, e poi e' indizio di nobilta',
perche' l'usare bene la metafora significa il percepire con la mente il concetto affine.
Questo passo della poetica di Aristotele testimonia come anch'egli riconosca forme produttive di pensiero non riconducibili alla logica e
al sillogismo, e le veda come fonti di originalità e creatività, caratteristiche che non si possono apprendere con uno studio
sistematico, che invece permette a chiunque di imparare i principi della logica.
L'irrazionale
Poiche' la struttura della monade nasce dal rapporto aritmetico, se il rapporto aritmetico non e' possibile, non e' possibile neanche il
nascere di una struttura che permetta l'individuazione di un "uno" e l'unificazione, alla fine di questo processo, del sensibile. L'irrazionale
scuote la semplicita' di questo sistema e pone nuovi difficili problemi. I numeri interi non sono piu' sufficienti per descrivere ogni tipo di
rapporto. Anche nella musica, dove il metodo pitagorico ha trionfato, si pone lo stesso problema poiche' , se si vuole dividere l'ottava, cioe'
il rapporto A:2A in due intervalli uguali, si dovra' trovare una grandezza X per la quale
A : X = X : 2A.
Questa proporzione non può essere risolta con numeri interi: qualunque valore intero si attribuisca ad A ed a X non si riuscira' mai ad ottenere
X²=2A²
(espressione equivalente alla proporzione precedente)
poiche' nessun numero intero quadrato puo' essere scritto come somma di due numeri interi quadrati e uguali tra loro. Geometricamente l'equazione si
risolve facilmente prendendo la diagonale del quadrato di lato A, ma la grandezza cosi' costruita non puo' essere misurata a partire da una monade che
ne misuri anche il lato A. Insomma tra aritmetica e geometria, che pure parevano identificarsi, si stende un fiume che terra' le due discipline separate
per moltissimi secoli privilegiando per la sua potenza di calcolo la geometria e le sue costruzioni. La riga e il compasso, piu' potenti delle palline
dell'abaco, ne prenderanno il posto. Resta tuttavia un algoritmo (quello delle frazioni continue basato sull'algoritmo euclideo probabilmente noto da
tempi antichissimi), che, a partire dalla diade iniziale, dalle due grandezze il cui rapporto non e' analogo ad alcun rapporto tra numeri interi,
permette di costruire un'alternanza di rapporti interi che approssimano sempre piu' per eccesso e per difetto il rapporto dato. Ne nasce cio' che oggi
diremmo una successione di Cauchy razionale che ha come limite il rapporto iniziale. La diade primogenita definisce ancora un ben definito "principio
generatore" un processo che consente in ogni caso di costruire la successione di Cauchy. Quanto basta per stabilire un ponte, se pure con infinite
arcate, tra l'aritmetica cioe' i numeri (interi) e le grandezze, cioe' la geometria. Una base coerente, crediamo anche di una certa consistenza
didattica, con la quale, prescindendo dal metodo di Eudosso, costruire per via algoritmica i numeri reali. Ma lo sviluppo stesso della teoria
matematica fondata dai pitagorici, la sua ricchezza concettuale porra' difficolta' ancora maggiori del problema dell'incommensurabilita', sicuramente
ben chiare a Filolao ed Archita.
Ad esempio: supponiamo di voler dividere in tre intervalli uguali l'ottava, cioe' il rapporto A : 2A,. Si dovra' allora trovare una grandezza X e
una grandezza Y in modo che:
A : X = X : Y = Y : 2A
cio' e' equivalente a risolvere l'equazione
X³=2A³
la cui soluzione X non solo non e' commensurabile con A ma neppure e' costruibile con riga e compasso. In questo caso dunque, come nel caso precedente,
l'aritmetica dei numeri interi non basta a risolvere la questione, ma anche il ben piu' potente strumento geometrico si rivela inefficace. Archita
38
per risolvere questo problema immagina una costruzione molto ardita ed ingegnosa che fornisce la soluzione come intersezione di una sfera con un
cilindro e un toro. Anche Eratostene troverà una sua soluzione, progettando uno strumento meccanico, il mesolabio, capace di determinare
la soluzione X come punto particolare di una scala graduata.
Nel dialogo che segue proponiamo una dimostrazione "secondo natura"dell'incommensurabilità della diagonale del quadrato col lato,
cercando di rispettare lo spirito e la mentalità pitagorica e di rappresentare la presa di coscienza di una antinomia profonda destinata
a scuotere il pensiero scientifico e filosofico greco.
Il Primo Quadrato
Brontino: ...vedi, Deonono come il tre è il Primo Triangolo e ha in potenza tutte le proprietà dei dispari, , così il quattro è
il Primo Quadrato, e come tale contiene in sè, in potenza, i numeri tutti, dal momento che l'1 e il 2 e il 3 e il 4 ch'egli contiene fanno il numero
10, e dopo il 10 i numeri si ottengono tutti decina dopo decina, senza nient'altro aggiungere.
Deonono: e contenendo i numeri tutti contiene in potenza anche tutti i rapporti numerici?
Brontino: certo, e prima di lui li contiene l'uno, che è forma delle forme, come insegna il Maestro.
Deonono: quel che non sai, Brontino, è che i rapporti espressi in potenza dal Primo Quadrato non sono tutti i rapporti...
Brontino: parla piano! Che eresie vai dicendo? E cosa poi rende palese questa mostruosità che pensi di farmi credere?
Deonono: è proprio quel tuo Primo Quadrato a dircelo, Brontino, e se stai quieto lo faremo parlare, e sarà lui a convincerti.
Brontino: sei pazza, Deonono ma la pietà degli Dei è grande e saprà risparmiarti, appena avrai finito di mostrarmi quanto dici,
se ammetterai i tuoi errori.
Deonono: guarda con me, Brontino Tu sai che il Primo Quadrato costruisce tutti i quadrati di lato pari

Brontino: certo, Deonono, ma cosa ha in comune questo fatto legato all'illimitato e al divino, con l'eresia di poc'anzi?
Deonono: aspetta, Brontino, non ti impazientire. Tu sai anche che il Primo Quadrato non può costruire un quadrato di lato dispari.
Brontino: anche questo è palese, mia cara Deonono, ma non mostra proprio nulla.
Deonono: ...e ancora che se con le unità di un quadrato dispari provi a far tanti Primi Quadrati quanti ne vengono, quando avrai finito
avanzerà sempre una unità
Brontino: come fai a sapere che avanzerà sempre e solo una unità, Deonono? Perchè non ne possono avanzare due, o tre?
Deonono: guarda tu stesso, caro compagno
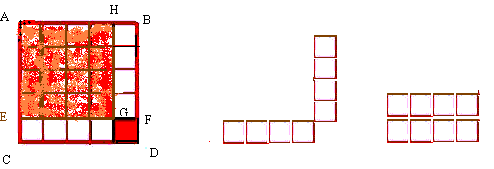
convieni con me che il quadrato dispari ABGD, tolto lo gnomone, darà il quadrato pari AEQH, costruito interamente quindi da Primi Quadrati?
Brontino: sicuro, mia sprovveduta amica
Deonono: e che lo gnomone, tolta l'unità che ho segnato, darà due volte il suo braccio pari?
Brontino: certo...
Deonono: e che queste sue braccia chiuse generano Primi Quadrati, senza alcun resto?
Brontino: non si può negare, dolce compagna. E vedo compiersi la prova di quel che mi volevi mostrare: se con le unità di
un quadrato dispari si costruiscono tanti Primi quadrati quanti è possibile, ne avanzerà sempre e solo una unità. E' singolare
questo, ma come ci avvicina all'eresia che ti ho sentito dire prima?
Deonono: non avere fretta, Brontino, chè la strada è ancora lunga e gli dei non ci saranno benevoli, ne son certa!
Guarda qui: vedi questo quadrato? Credi che ne possa esistere uno doppio?
Brontino: ah! Povera amica mia! Ti sei persa in questa ricerca, e non riuscendo a trovare un quadrato doppio di uno dato, smetti di credere
nella potenza creatrice del numero? Ma guarda, ecco come si trova quello che vai cercando:
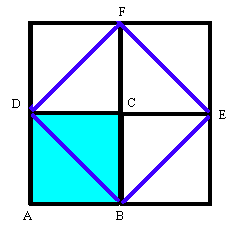
come puoi ben vedere, DBEF è doppio di ABGD! E ancora una volta è il primo quadrato che permette ti generare una tale meraviglia.
Deonono: sei sempre pronto a interrompermi, Brontino, e così mi fai ripetere le cose mille volte! Ecco, hai trovato il doppio di un quadrato,
che sia quadrato anch'esso. Questo è inconfutabile. Ma, dimmi, pensi che esistano due numeri sui quali costruire tali quadrati?
Brontino: che dici, donna? Come puoi mettere in dubbio che esistendo i lati, e tu li vedi con i tuoi occhi, non esistano anche i due numeri
appropriati a descriverli?
Deonono: non ti scaldare, Brontino, che ti servirà tutta la forza del tuo spirito, tra poco, per accogliere le verità che ti
sto dicendo. Allora ammetto che questi due numeri esistano....
Brontino: diavolo di una donna! Mi avevi fatto preoccupare, per un attimo!
Deonono: e se esistono, potrò vedere se sono entrambi pari, o uno pari e uno dispari.
Brontino: ..te lo concedo...
Deonono: e se sono entrambi pari, posso cambiarli con le loro metà, e ottenere ancora una coppia che possa descrivere il lati dei quadrati
come la precedente. E così fino a che uno di loro non sia dispari.
Brontino: e perchè non dispari entrambi?
Deonono: perchè mio caro Brontino, il quadrato più grande, essendo doppio di una data quantità, è senz'altro pari, e
allora anche il suo lato deve essere pari.
Brontino: la cosa comincia a imbrogliarsi, ma guarda che sono ben capace di tenerti dietro senza farmi confondere. Hai detto insomma che
il quadrato DBEF, dopo essere arrivati a numeri che non possono essere più dimezzati, deve avere per forza il lato pari e che il quadrato
ABGD lo deve avere per forza dispari.
Deonono: giusto. In altre parole ho detto che il quadrato DBEF è costruito dal Primo Quadrato, essendo pari, e che da ABGD invece,
essendo dispari, si possono ricavare un certo numero di Primi quadrati, con l'avanzo di una unità.
Brontino: certo, e allora? Deonono: ma non capisci, Brontino? Se raddoppio il quadrato ABGD avrò il doppio di quei Primi quadrati,
e mi avanzeranno
due unità. E come posso, con quei Primi quadrati e due unità coprire DBEF, che è fatto interamente di Primi quadrati?
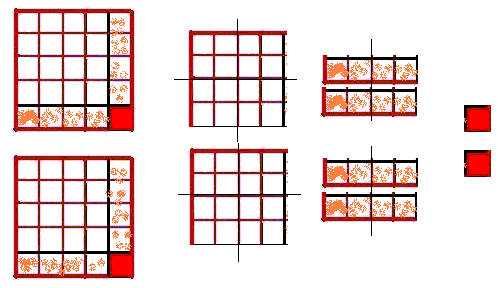
Come vedi, mio povero Brontino è impossibile che il doppio delle unità che misurano il quadrato ABGD, possano anche misurare il quadrato
suo doppio, CDEF, fatto di Primi Quadrati: ci saran sempre due unità che non trovano posto!
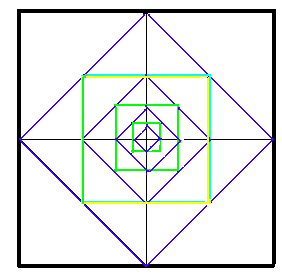
E così tu, mio maestro, e io, tua allieva, saremo per la vita legati da questo segreto divino, che apre al pensiero le porte di un mondo
misterioso: il Primo quadrato, che in potenza contiene in sè tutti i rapporti, ma in potenza ne distrugge anche l'anima divina, negando loro
la partecipazione all'essenza della Monade, dell'Uno Infinito, mostrando l'esistenza di una infinita alterità da loro.
Ma finchè le mani del Maestro non lasceranno le nostre, caro compagno, saprò avanzare sicura oltre quelle porte, a dispetto di tutti
gli Dei e della loro furia.
|
|