|
1. Introduzione
Nella prima parte di questo lavoro abbiamo analizzato la insolita figura scientifica di Desargues e abbiamo interpretato il suo particolare
linguaggio matematico come un tentativo di guidare il pensiero attraverso le parole verso immagini nuove capaci di rappresentare lo spazio
che lui aveva immaginato e dove aveva collocato l'infinito. L'introduzione di punti all'infinito modifica non solo la struttura dello spazio
(del quale diventa impossibile, per motivi topologici, farsi una immagine globale) ma anche le figure che in quello spazio sono tracciate. Esse
infatti acquistano una particolare rilevanza proprio nel modo col quale si rapportano all'infinito. Da una lato dunque le figure euclidee, sempre
chiuse e limitate, vengono a perdere la loro centralità rispetto a quelle che toccano l'infinito, d'altro lato proprio questa loro
compattezza ne permetteva una rappresentazione attraverso un'immagine su un foglio di carta in grado di guidare l'intuizione geometrica. Ora
questa operazione diventa spesso impossibile e per questo Desargues cerca di creare nuovi strumenti che gli vengono suggeriti dalla sua pratica
di architetto, ingegnere e dalle suggestioni del disegno prospettico.
Per rendere la lettura di questa seconda parte del lavoro il più possibile indipendente dalla prima ricordiamo alcune definizioni di Desargues
ampiamente discusse in quella sede anche dal punto di vista cognitivo. Il tronco (tronc) è una retta (sempre pensata estesa
fino all'infinito dalle due parti) alla quale si appoggiano, in punti detti nodi, (neud) altre rette dette rami, (rameau). Un ramo,
o una sua parte, può essere dispiegato (déployé) o piegato (plié) sul tronco a seconda che si sovrapponga
o meno al tronco. I but sono i punti al finito o all'infinito dove si incontrano due rette. I segmenti di un ramo che vanno dal nodo a
un altro ramo sono detti ramoscelli (brin de rameau).
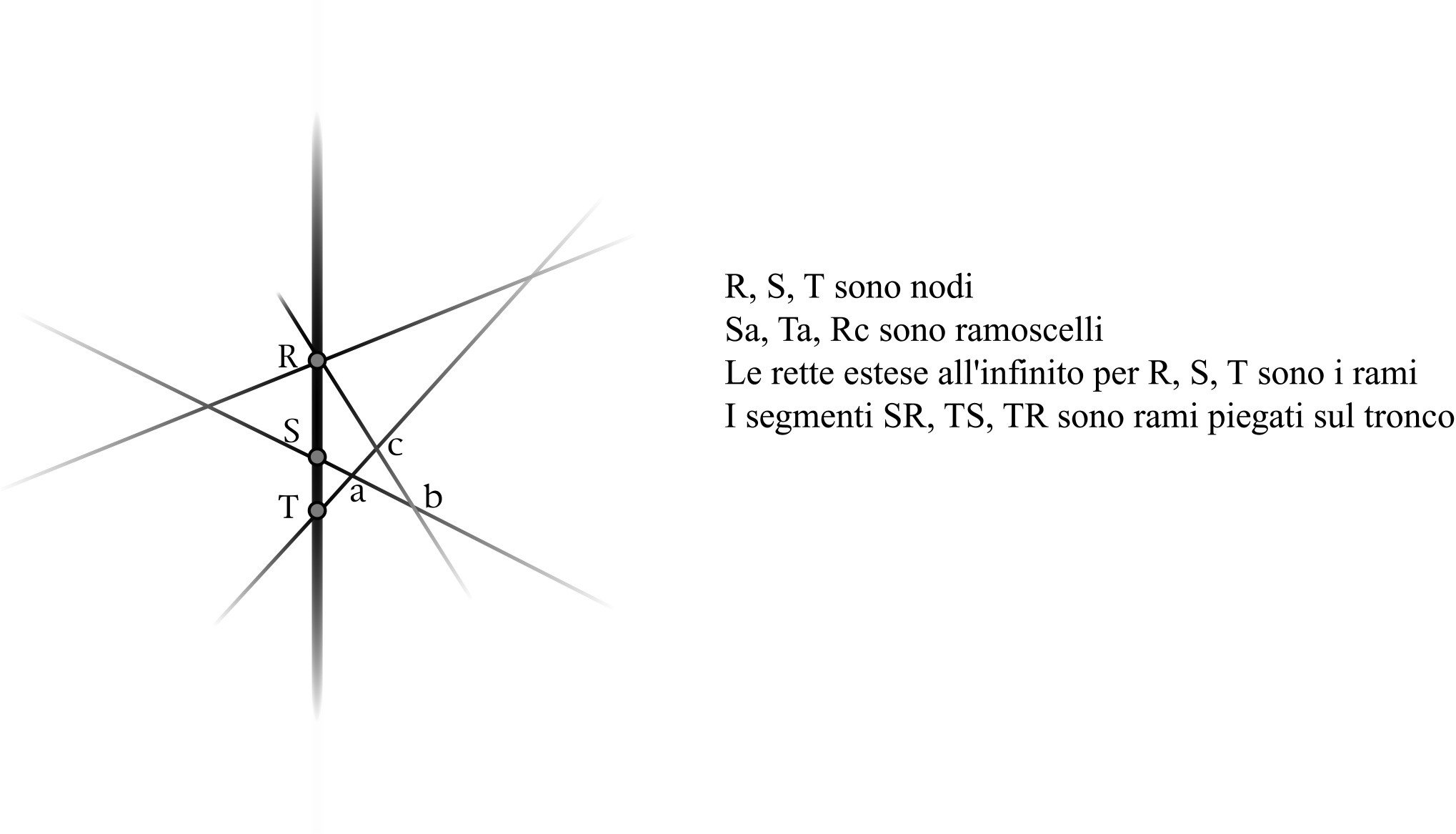
Immagine 1
Tre coppie di nodi di un tronco, AA',BB', CC' si dice formano una involuzione se, nel linguaggio di Desargues
1
, il rapporto tra rettangoli
relativi è uguale a quello tra i loro gemelli, se cioè
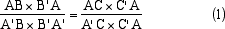
Dove con AB indichiamo la lunghezza con segno del segmento AB una volta orientato il piano e fissata una unità di misura. Si vede dunque
come, a questo livello, il concetto di involuzione sia di natura metrica o meglio affine coinvolgendo rapporti tra segmenti.
Nel corso di questo lavoro diamo, spesso in nota, le dimostrazioni dei teoremi che enunciamo essendo queste per la maggior parte
quelle fornite da Desargues, con il duplice scopo di fare una rassegna storica, il più possibile fedele, delle idee e tecniche
del geometra lionese, e indicare un percorso didattico che dalle involuzioni conduce, in uno spirito che a noi pare più semplice e
diretto, al teorema di Pascal sull'esagono inscritto in una conica, uno dei gioielli del pensiero matematico.
2. ''Ricentramenti cognitivi'' del teorema di Menelao
Il teorema di Menelao piano
2
è uno dei pochissimi prerequisiti su cui Desargues fonda le sue dimostrazioni, e per questo, ma soprattutto
per il modo nuovo con cui lui lo presenta, ha per noi particolare importanza. Il solo confronto, cui ora accenniamo brevemente, tra la sua
formulazione e quelle precedenti, mette in luce l'approccio nuovo, le dinamiche intuitive che vengono suggerite e fa capire come uno stesso
enunciato matematico possa arricchirsi, a seconda del modo in cui viene presentato, di significati profondi che vanno ben al di là di
una semplice esattezza formale.
Questo teorema non fa parte delle proposizioni dei 13 libri degli Elementi di Euclide, mentre lo troviamo nella Sferica di Menelao, matematico
e astronomo alessandrino del II secolo dopo Cristo, come lemma introduttivo per dimostrare un analogo teorema (oggi noto come teorema di Menelao)
nella geometria della sfera. Per questa via Menelao [9] riuscì a sviluppare una teoria quantitativa sui triangoli sferici e sui rapporti tra
le ''ampiezze'' dei lati, in un contesto, quello sferico, dove non esistono ''rette'' parallele. In quell'ambito ebbe a che fare con
concetti invarianti per proiezione, quali ad esempio quello di rapporto armonico
3
[9] , tipici di una geometria, come quella proiettiva,
che prescinde dal concetto di parallelismo. Le applicazioni astronomiche della geometria della sfera renderanno il teorema di Menelao di
grande utilità e per questo lo ritroviamo nell'Almagesto di Tolomeo [10]
4
dove viene applicato per calcolare, per via teorica, l'altezza
del Sole sull'orizzonte in un dato giorno dell'anno. E' questa la versione del teorema che Desargues cita e per questo la riproduciamo
letteralmente, come si trova nel testo di Tolomeo:
Se due rette AB, AG, che si incontrano in A, sono tagliate da altre due rette GD, BE, che si intersecano nel punto Z, dico che il rapporto
tra il segmento di retta AE ed il segmento di retta EG è uguale al rapporto tra il segmento di retta DZ e il segmento di retta ZG,
composto con il rapporto tra il segmento di retta BA ed il segmento di retta BD.
L'immagine che si forma è quella di due segmenti che si incontrano in A ai quali se ne aggiungono altri due che si incontrano in Z
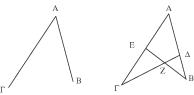
in questa situazione vale una certa relazione che lega i rapporti tra le lunghezze dei segmenti che nascono dall'intersezione delle
rette. Precisamente
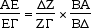
Fibonacci [11] nella sua Pratica geometrica, riporta il teorema di Menelao con l'uso delle stesse lettere latinizzate scelte da Tolomeo
(che probabilmente è stato la sua fonte) ma con una formulazione che richiama una diversa Gestalt
5
:
Se in un triangolo .abg. tracciamo delle rette .be. e .gd. che escono dagli angoli .b. .g. e se queste si incontrano nel punto .z. allora,
se è noto il rapporto tra .ge. e .ae. e tra .bd. e .ad. allora è noto anche il rapporto tra .bz. e .ze. e tra .gz. e .zd.
La configurazione di Menelao, data dall'intersezione di quattro segmenti, si trasforma in un triangolo fisso contenente due segmenti. .gd. e .be.,
uscenti dai vertici g e b, ed intersecantesi in .z.
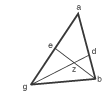
Notiamo che il triangolo è curiosamente una figura ridondante in rapporto all'enunciato del teorema, ma la sua ''chiusura'' crea
buona struttura gestaltica, che si richiama facilmente alla memoria e che guida la ricostruzione delle possibili relazioni numeriche. Le
relazioni che legano i vari rapporti venivano all'epoca usate meccanicamente nella soluzione di problemi numerici e commerciali ampiamente
riportati nel Liber Abaci con il nome di regula baracti
6
o regula sex quantitatum, perché date cinque di sei
quantità incognite,
porta a ricavare la sesta, e questo ricentramento del testo poteva essere funzionale a una pratica di memorizzazione ad uso più di
mercanti che di matematici.
Nel giardino di Desargues il teorema di Menelao cambia ancora fisionomia, si inserisce nel nuovo sfondo che lui ha immaginato, tocca l'infinito
7
Quando su una retta HDG, pensata come tronco, per tre punti H,D,G, pensati come nodi, passano tre rette come rami dispiegati Hkh, Dqh, Gqk,
qualunque getto Dh di qualunque di questi rami Dqh, che esce dal suo nodo D e arriva al ramo Hkh, sta al suo getto accoppiato Dq che esce
dallo stesso nodo D arriva al terzo ramo Gqk, nello stesso rapporto del rapporto composto tra i getti su ciascuno degli altri due rami
convenientemente ordinati...
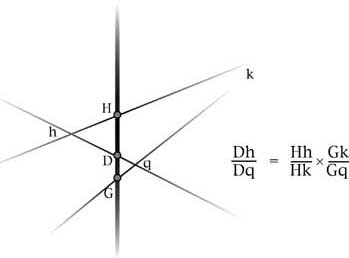
Immagine 2
Segue la dimostrazione che è essenzialmente uguale a quella che riporta Tolomeo.
L'accento del teorema è messo sul tronco, sui tre nodi e sui rami che si dispiegano dal tronco, creando una immagine dinamica nella quale
vediamo le varie configurazioni che questi rami possono assumere ruotando attorno ai nodi, liberi di diventare anche paralleli tra
loro. La ''regola delle sei quantità'' è ora presentata in modo diverso: tra le 4 rette che intervengono nel teorema, ne viene
fatta emergere una in particolare mediante l'attribuzione di un nome specifico
8
, il tronco. In questa lettura la formula che lega i vari
rapporti coinvolge così solo i brin , i ramoscelli, che escono dai nodi H, D, G, e che vanno ai but h, k, q, punti in cui questi
ramoscelli arrivano ad incontrare gli altri rami. Le grandezze hk, hq , qk, che non hanno un nome particolare che le definisca, non hanno
alcuna parte nella formula
9
.
L'immagine che in questo modo si forma ci permette di intuire come nulla cambi anche nel caso in cui qualche punto vada all'infinito. Comunque
i rami si dispieghino, hanno sempre un comune but, in virtù del principio che Desargues premette all'inizio del Brouillon
secondo il quale due rette nel piano hanno sempre un comune but
10
. Anche la relazione algebrica, per ragioni di continuità, deve
avere una naturale ''degenerazione'' non difficile da trovare. Desargues nota esplicitamente
11
:
Ci sono molte cose da osservare in questo enunciato quando due dei tre rami sono paralleli tra loro; quando al tronco ci sono due nodi
uniti in uno e ciò che ne deriva dove il pensiero non vede più nulla
Ciò che accade, infatti quando k tende all'infinito è che il rapporto tra Gk e Hk tende a 1 e la regola si riduce alla uguaglianza
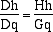
che esprime la proporzionalità dei lati corrispondenti in due triangoli HhD e GqD che diventano simili quando il ramo per H è
parallelo a quello per G. Il teorema sulla proporzionalità dei lati nei triangoli simili, diventa una degenerazione del teorema di
Menelao quando parte della figura va all'infinito. I teoremi stessi diventano oggetti dinamici, degenerano uno nell'altro in un quadro
complessivo dove il rapproto con l'infinito genera un nuovo ordine, nuova conoscenza.
Ancora più ardita è la degenerazione ottenuta quando un nodo vada a sovrapporsi ad un altro: la forma cambia completamente,
il suo significato sfugge, ''l'entendement ne voit goute'' e la figura limite, con la formula che si porta dietro, viene a dipendere dal
modo con cui i due nodi, e i rami per essi, vanno a sovrapporsi tra loro.
In questo quadro l'oggetto euclideo, il triangolo, appare solo come caso accidentale e non ha alcun ruolo. In tutto il Brouillon il
termine ''triangolo'' non è mai usato, se non in contesti molto particolari dove si applicano i risultati della teoria in situazioni
standard. Lo stesso teorema oggi noto come teorema di Desargues sui triangoli omologhi, nell'enunciazione originale
12
non contiene il termine
triangolo. Questo termine richiama alla mente lati e angoli che irrigidiscono la figura entro confini di un foglio mentre per Desargues
un ''triangolo'' è una terna di rette che non fanno parte di uno stesso fascio e che può toccare l'infinito.
Appare dunque come l'universo che Desargues ha in mente sia completamente diverso da quello euclideo, sia nella definizione dell'ambiente
che per le forme che in questo ambiente vivono, e come sia di conseguenza opportuno rimuovere rigidità mentali legati a una consolidata
consuetudine per far emergere le nuove concezioni. Crediamo che proprio l'uso del nuovo linguaggio, che più è stato avversato,
avrebbe potuto aprire le porte della comprensione alla geometria proiettiva. Purtroppo la storia ha avuto esiti diversi e le proposte di
Desargues sono state ignorate e perdute per quasi 200 anni e oggi che questa materia si è imposta con i suoi oggetti e le sue definizioni
seguendo strade diverse diventa improponibile tornare alle origini. Ci resta il significato esemplare del metodo desarguesiano, la sua attenzione
didattica nei confronti delle immagini mentali, il suo legame con la concretezza e l'intuizione anche nelle situazioni più astratte, ci
resta lo stimolo a rivedere criticamente il nostro stesso lavoro di insegnanti.
3. Menelao si piega sul tronco
I vari movimenti che Desargues suggerisce presentandoci il teorema di Menelao e il suo linguaggio metaforico, ci hanno fatto pensare a una
ulteriore drastica degenerazione ottenuta ''chiudendo'' tutta la configurazione sul tronco e cercando di capire il modo in cui la regola
algebrica si modificasse di conseguenza. Se fossimo riusciti a trovare un risultato interessante avremmo capito il motivo per cui Desargues parla
di rami dispiegati e piegati sul tronco, questa metafora, apparentemente enigmatica, sarebbe diventata ''produttiva''. Dato il contesto, abbiamo
pensato a una proiezione centrale.
L'immagine dinamica, che Desargues ci mostra, di questi rami che si piegano e dispiegano dal tronco, ci ha confermato nell'idea di proiettare
sul tronco la configurazione relativa al teorema di Menelao. Così facendo i getti si stendono nell'unica dimensione della retta e otteniamo
in questo modo sei punti: i tre nodi e le proiezioni dei tre but. Sei punti che possiamo accoppiare tra loro in modo naturale, accoppiando
ad un nodo la proiezione del but comune ai due rami che non passano per il nodo stesso. Ecco la nostra nuova immagine: proiettando sul
tronco da un punto d scelto ad arbitrio, i but a, b, c e accoppiandoli con i nodi A, B, C otteniamo le tre coppie AA', BB', CC'.
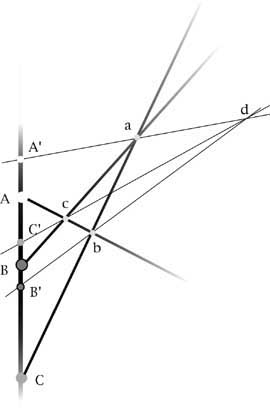
Immagine 3
Se ora cerchiamo di vedere come si trasforma la relazione di Menelao ci rendiamo conto, con soddisfazione, che anch'essa continua a valere
semplicemente sostituendo i getti dispiegati dal tronco con le loro proiezioni
13
: precisamente la relazione
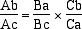
degenera nella:
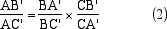
e quest'ultima relazione, che è equivalente alla (1), ci dice che le tre coppie AA',BB',CC' formano una involuzione.
Non possiamo dire se Desargues conoscesse o meno questo risultato perché non è mai esplicitamente enunciato, né lo abbiamo
trovato nella letteratura corrente; non possiamo neanche dire se questa possa essere stata la strada con la quale lui è pervenuto
all'idea di involuzione. Resta comunque il fatto che il teorema di Menelao ''piegato sul tronco'' produce 6 punti legati nella forma
dell'involuzione inquadrando sotto una nuova luce, anche dal punto di vista didattico l'intera materia che, in questa maniera, crediamo
possa essere in parte rivista. A conforto della nostra congettura, abbiamo trovato, non senza emozione, nel Brouillon una
incomprensibile incongruenza che potrebbe aiutarci a entrare nel pensiero di Desargues. Nella formulazione del suo celebre teorema
sulla involuzione definita su un retta da un fascio di coniche, sul quale torneremo più avanti, Desargues aggiunge alla fine un
enunciato (di dimostrazione ovvia) completamente inutile, mai usato nel seguito, nel quale il linguaggio non è coerente con le
definizioni da lui stesso date in precedenza. Come se questo enunciato, frutto di precedenti considerazioni, poi superate da nuove idee,
gli fosse sfuggito per sbaglio nel Brogliaccio. Ma proprio questo eventuale sbaglio può aiutarci a chiarire la genesi di queste
metafore.
Ecco il testo
14
Se due rette di confine BCN , EDN sono parallele tra loro, il rettangolo dei getti dispiegati IB, IC sta al suo relativo il
rettangolo KD, KE come il rettangolo dei getti piegati sul tronco IQ, IP gemello del rettangolo IB, IC sta al suo relativo il rettangolo
dei getti piegati sul tronco KQ, KP gemello del rettangolo KD, KE cosa che è evidente dal parallelismo di questi rami di confine BC,
DE.
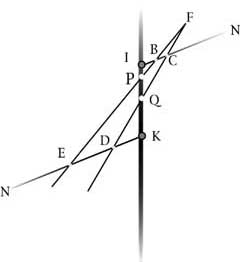
Immagine 4
Intanto le definizioni di rettangoli gemelli e rettangoli relativi date in precedenza si riferiscono sempre a getti piegati sul tronco
15
, mentre
ora ci si riferisce ai rettangoli di lati IB, IC (dispiegati) e IP, IQ (piegati) come fossero rettangoli gemelli. La stessa cosa avviene sul
ramo KN. Ma la cosa più importante e molto chiara è che l'operazione di piegare un getto sul tronco consiste proprio nella proiezione
centrale (in questo caso la proiezione dal punto F).
Tornando alle involuzioni, emerge una cosa importante: abbiamo ora due modi per riguardare l'involuzione uno algebrico e l'altro geometrico. Quello
algebrico consiste nel verificare se i 6 nodi sono posizionati in modo tale da verificare l'uguaglianza (1) (o la (2) a essa equivalente) e queste
formule permettono dati 5 dei sei nodi in involuzione di trovare in modo univoco la posizione del sesto. Da un punto di vista geometrico invece
tre coppie nodi di un tronco formano una involuzione se esiste una configurazione grafica come quella rappresentata dall'immagine 3 che lega
tra loro i vari nodi. Il fatto, ottenuto per via algebrica che 5 nodi individuano univocamente la posizione del sesto, dimostra che , qualunque
sia la configurazione per i 5 nodi assegnati, la posizione del sesto non cambia.
Dati ad esempio A, B, C, A', B' possiamo trovare graficamente il nodo C' in modo che le tre coppie AA', BB', CC' formino una involuzione. Lo
possiamo fare in infiniti modi, anzi, in ''infinito a tre'' modi, per essere più precisi. Possiamo dispiegare arbitrariamente i rami
per A, B, C, e trovare così i but a, b, c comuni alle tre coppie di rami. Collegando poi a con A' e b con B' troviamo il centro
di proiezione d che ci permette, proiettando c, di trovare C' . Il punto C', lo stesso punto C', è determinato comunque si siano dispiegati
i tre rami iniziali, proprio perché le due coppie AA' e BB' individuano un'unica involuzione.
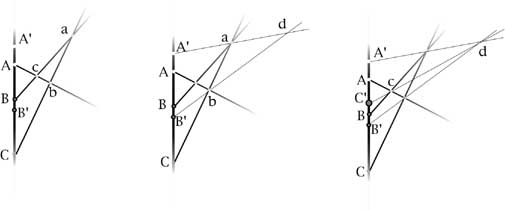
Immagine 5
figura animata
Dunque se 5 di 6 nodi in involuzione sono dati, il sesto è determinato non solo tramite una relazione numerica che ne fissa
la posizione rispetto agli altri, ma anche da una configurazione grafica che coinvolge solo il concetto di retta, di punto (al finito
o all'infinito) con le proprietà grafiche di appartenenza. Per questa via è possibile fondare la geometria proiettiva
indipendentemente dal campo numerico di base, partendo da assiomi grafici così come è stato fatto nel magnifico
trattato di Enriques del 1904, Lezioni di geometria proiettiva.
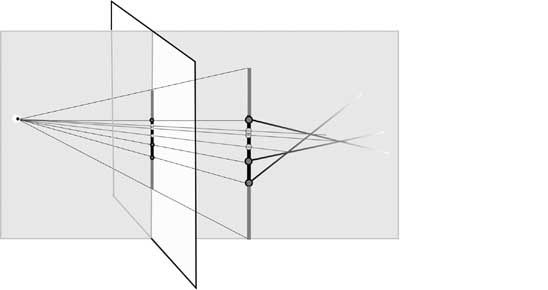
Immagine 6
figura animata
Osserviamo infine come la trasformazione che proietta sul tronco una data configurazione sia familiare all'attitudine del pittore a
rappresentare un oggetto tridimensionale nelle due dimensioni del quadro. Anche in questo caso il teorema di Menelao che si dispiega
nelle due dimensioni, si proietta nell'unica dimensione del tronco conservando tuttavia una determinata traccia della sua genesi, questa
traccia è l'involuzione: la proiezione dei nodi e quelle dei tre but accoppiati tra loro.
4. Il teorema del rameto
L'invarianza proiettiva del concetto di involuzione, intuito in questo modo, viene rigorosamente dimostrato da Desargues
nel ''teorema del rameto''. Un rameto è formato da un tronco che contiene sei nodi in involuzione dai quali escono sei
rami con uno stesso but. Se un secondo tronco interseca i sei rami del rameto in sei nuovi nodi, anche questi formano
una involuzione.
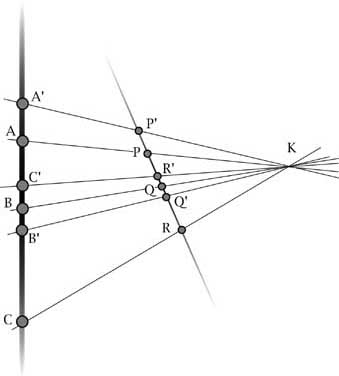
Immagine 7
Il teorema può essere dimostrato in modo tradizionale, senza uscire dal piano del rameto, cercando di provare che
la relazione (1) non cambia forma durante la proiezione, cioè si trasforma nella relazione
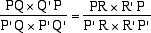
e questo può essere fatto considerando, sullo stesso piano del rameto, varie configurazioni di rami e applicando varie volte
e in modo opportuno il teorema di Menelao. E' questo il modo che segue Desargues, come volesse procedere nelle sue dimostrazioni
coi piedi di piombo. Possiamo tuttavia, in questo caso, proporre una dimostrazione che non faccia uso delle relazioni algebriche che
caratterizzano le involuzioni e che pare Desargues voglia indicare più avanti
16
. Cominciamo col dispiegare dal tronco, tre rami
per A, B e C appartenenti a un nuovo piano a , che immaginiamo orizzontale e costruiamo su questo piano l'intera
configurazione che
caratterizza l'involuzione iniziale. Alziamo ora una piramide col vertice in K e base sul quadrangolo abcd.
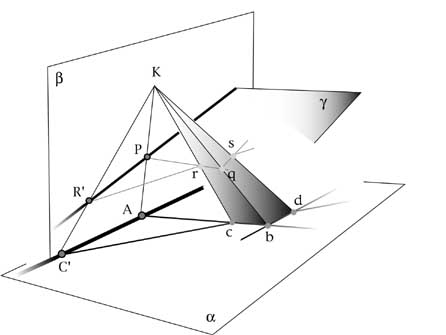
Immagine 8
Prendiamo ora un nuovo piano g che passi per la retta che contiene i nodi PP', QQ', RR'. Tale piano interseca
la piramide in un ulteriore
quadrangolo pqrs che si proietta, punto per punto, retta per retta, sul quadrangolo iniziale e che trasporta quindi la configurazione del
piano a definita dall'involuzione iniziale, in una analoga configurazione sul piano g che
conferisce quindi alle tre coppie PP', QQ', RR'
la forma di involuzione.
Questa dimostrazione si fonda sul fatto che la proiezione centrale conserva l'allineamento e quindi ogni configurazione grafica formata da
rette e loro intersezioni, conformemente alla geometria della visione e all'intuizione del pittore.
Abbiamo trovato in questo modo una particolare configurazione tra i punti di una retta che non cambia dispiegando arbitrariamente dal tronco
i tre rami per A, B, C e cambiando il punto di vista. Le involuzioni diventano uno strumento per allenare il pensiero su un terreno che gli
sia proprio (quello euclideo) ma anche potenziarlo verso la geometria dell'infinito.
5. La proprietà meravigliosa
Possiamo pensare le involuzioni come un modo per accoppiare i punti di una retta o meglio come un modo per far corrispondere a un dato
punto X un punto X' e a X' lo stesso punto X, cioè, come si dice oggi, ad una trasformazione involutoria della retta in sé. Date
due coppie di punti corrispondenti AA' e BB' (eventualmente doppi) l'involuzione, cioè la trasformazione della retta in sé, è
univocamente determinata sia sul piano analitico, tramite la formula (1), sia su quello sintetico proprio di Desargues, tramite una costruzione
grafica che abbiamo vista nel paragrafo precedente: il punto X' corrispondente di X sarà quel ben determinato punto per il quale le tre
coppie AA',BB', XX' fanno parte di una medesima involuzione. L'involuzione può essere definita, oltre che dalle due coppie di punti AA'
e BB', anche da una coppia di punti e una coppia di rette indicate in grigio nell'immagine seguente. In questo caso la costruzione è
identica al caso precedente e viene fatta a partire dai punti B e B' nei quali le rette date incontrano il tronco, ma ne cambia radicalmente
l'interpretazione. La coppia di rette è pensata come una ''curva di ordine due'' cioè come una configurazione che interseca una
qualunque retta in due punti ed è solo questa la proprietà che viene usata per costruire l'involuzione.
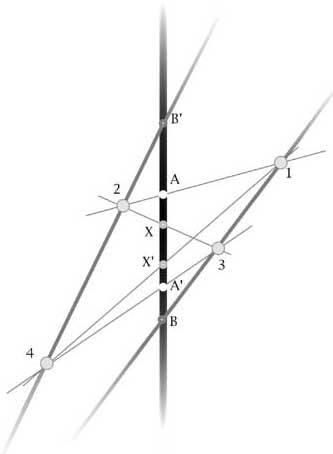
Immagine 9
Si comincia col dispiegare un qualunque ramo per A, che incontra la coppia di rette nei punti 1 e 2. Si congiunge 2 con X e si trova il punto 3,
si congiunge 3 con A' e si trova il punto 4, si congiunge 4 con 1 e si trova il punto X' che cercavamo, trasformato di X mediante l'involuzione
definita dalle coppie AA', BB' o dalla coppia di punti AA' e dalla coppia di rette fissate. Il punto X' che abbiamo costruito non dipende
dai (infinito a uno) modi con cui si è dispiegato il ramo da A o, equivalentemente, dalla posizione del punto 1 sulla coppia di
rette. Abbiamo una involuzione definita dalle due rette e dai due punti AA' indipendente da come abbiamo ''inscritto'' un quadrangolo 1,2,3,4
nelle rette stesse.
Questa immagine che sembrerebbe riproporre la situazione precedente ci spinge, in realtà in una direzione nuova molto importante. Una coppia
di rette possiamo infatti pensarla, come fa Desargues, come una conica degenere ottenuta segando il cono con un piano che passa per il suo
vertice. Ora tutte queste figure si ottengono l'una dall'altra con continuità, muovendo con continuità il piano sezione. Sembrerebbe
dunque naturale estendere la costruzione precedente, che è invariante per proiezioni, anche al caso di una qualunque conica.
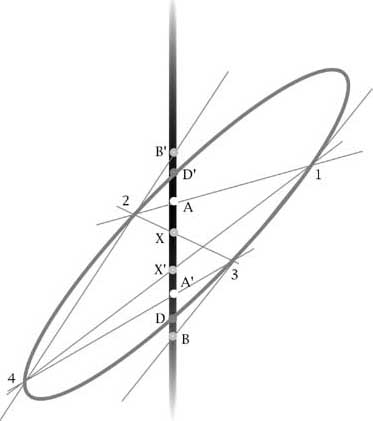
Immagine 10
Desargues riesce di fatto a dimostrare che una qualunque conica, che passi per i 4 punti 1,2,3,4 interseca il tronco in una ulteriore
coppia DD', che insieme ad AA', BB', XX', appartiene alla stessa involuzione, legando in questo modo, con una geniale intuizione, le involuzioni
alle coniche. Questo risultato è quello che Pascal chiamerà proprieté merveilleuse
17
il cui primo inventore è Desargues, lionese, uno dei più grandi spiriti dei suoi tempi, dei più versati verso
le matematiche e in particolare verso le coniche i cui pochi scritti su questa materia hanno dato un'ampia testimonianza a coloro
che hanno voluto capirne il significato: devo confessare che io devo il poco che ho trovato su questa materia ai suoi scritti e che h
o cercato d'imitare per quanto mi è stato possibile il suo metodo su questo soggetto.
Lo stesso Poncelet
18
, che non conosceva Desargues, parlerà di questo teorema come un des plus féconds qui existent sur les
coniques per le numerosissime conseguenze che esso comporta.
Possiamo vedere anche come, fissata una conica degenere o non degenere e due nodi AA' su un tronco, resta individuata univocamente una
involuzione, ottenuta sia che la conica intersechi in DD' il tronco, sia che non lo incontri, la quale involuzione, con la stessa costruzione
di prima, permette di trovare il coniugato X' di un qualunque nodo X comunque si voglia dispiegare da A il ramo A1:
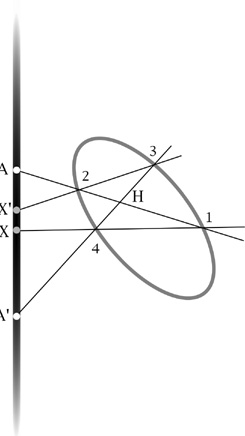
Immagine 11
In nota
19
diamo un cenno della dimostrazione di Desargues di questo fatto e della proprieté merveilleuse poiché essa introduce
per la prima volta nella storia della matematica un metodo dimostrativo molto fecondo che consiste nel trasformare una figura in un'altra
più semplice, per la quale sia possibile dimostrare la proprietà che interessa, la quale, se invariante rispetto alla
trasformazione effettuata, resterà valida anche per figura più complessa iniziale. In questo caso la trasformazione è
una trasformazione proiettiva che permette di trasferire su una qualunque conica proprietà valide per una circonferenza ed invarianti
per proiezione.
6. Mysterium hexagrammaticum
La teoria delle involuzioni così come è stata abbozzata nelle sue linee essenziali nel Brouillon di Desargues, permette
di dimostrare facilmente, come vedremo più avanti, il teorema attribuito a Pascal sull'esagono inscritto in una conica. Pascal, che
è stato allievo di Desargues, all'età di soli 16 anni, nel 1640, pubblicò un saggio nel quale enunciava alcune proprietà
delle coniche, tra cui il teorema secondo il quale un qualunque esagono inscritto in una circonferenza ha i lati opposti che si intersecano in tre
punti allineati, proprietà che poi estende, molto probabilmente col metodo di Desargues, al caso che l'esagono sia inscritto in una conica
qualunque. Il saggio, di sole 3 pagine, non contiene le dimostrazioni, ma si suppone, per quanto testimonia lo stesso Pascal, fossero fortemente
influenzate dalle idee e dai metodi di Desargues. Poncelet riferisce
20
[8], senza indicare la fonte, che Descartes avrebbe attribuito questo teorema
allo stesso Desargues. Una conferma indiretta di questo si può trovare in una lettera di Beaugrand
21
[2], nella quale questi risolve alcuni
problemi posti da Desargues e che Desargues poteva risolvere coi suoi nuovi metodi. Il problema consisteva nel costruire una conica passante per
dati punti (eventualmente sovrapposti), problema che, come è noto, si risolve facilmente usando il teorema di Pascal. In questo modo oggi
i programmi di computer grafica calcolano e disegnano la conica passante per 5 punti assegnati.
Vogliamo ora proporre una dimostrazione molto semplice di questo teorema che non abbiamo trovato in letteratura e che si basa sulla nozione di
involuzione e sui metodi di Desargues.
Consideriamo un esagono di vertici 1,2,3,4,5,6 inscritto in una conica, eventualmente anche degenerata in due rette. Vogliamo dimostrare che
le coppie di lati opposti 1-2 con 4-5, 2-3 con 5-6, 3-4 con 6-1 si incontrano in tre punti P, Q ed R allineati.
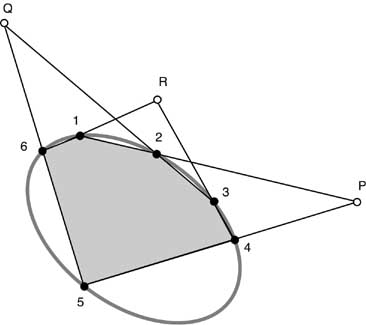
Immagine 12
Consideriamo il tronco definito dalla retta PQ e l'involuzione che il quadrangolo 1,2,3,6, definisce sul tronco:
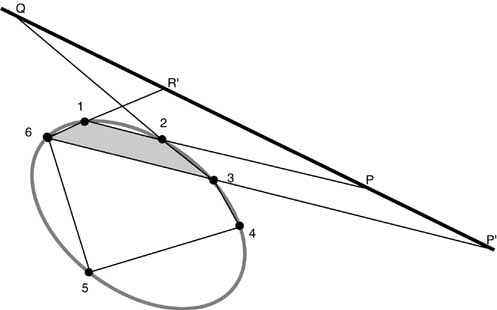
Immagine 13
P risulta coniugato a P' e Q al nodo R' ottenuto intersecando il tronco con il lato 6-1.
Consideriamo ora l'involuzione definita dal quadrangolo 3,4,5,6
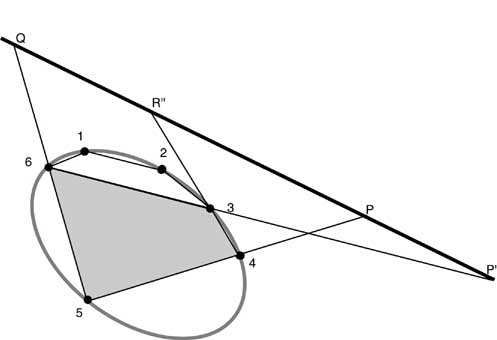
Immagine 14
abbiamo ancora che P è coniugato con P' e Q è coniugato con R'' essendo R'' il nodo in cui il lato 3-4 interseca il tronco. Dato
che le due involuzioni sono definite da una stessa conica e dalla stessa coppia PP', coincidono e quindi Q ha lo stesso coniugato nei due
casi. Ne segue che R' = R'' cioè che il lato 3-4 interseca il tronco nello stesso nodo R nel quale lo interseca il lato 1-6. Ne segue
ancora che il nodo R, intersezione dei due lati, si trova allineato sul tronco a P e a Q.
Questa dimostrazione, molto semplice e naturale se pensata nello spirito desarguesiano, si basa sul concetto d'involuzione, centrale nel suo
approccio, e corrisponde all'enunciato originale così come è formulato da Pascal [7] nel quale, anziché affermare che
i punti P, Q ed R sono allineati, si conclude che, definiti P e Q come abbiamo fatto qui, le rette per PQ, 1-6 e 3-4 passano da uno stesso
punto.
Le dimostrazioni elementari del teorema di Pascal più diffuse nei vari manuali di geometria proiettiva, considerano prima
il caso che la conica sia un cerchio, per poi estendere il teorema nel caso generale. Per il cerchio si usa il concetto di birapporto
tra quattro rette e la sua invarianza, muovendo il centro del fascio di rette sulla circonferenza. Il caso degenere, quando la conica si
spezza in due rette, caso che corrisponde al teorema di Pappo, richiede, seguendo questa via, una dimostrazione particolare. La dimostrazione
che qui abbiamo proposto vale in ogni caso e ci pare concettualmente più semplice e diretta.
Bibliografia
[1] N. Poudra, Oeuvres de Desargues réunies et analysées, 2 Volumi , Paris, 1864
[2] R. Taton, L'oeuvre mathématique de G. Desargues, Presses Universitaires de France, 1951 (seconda edizione rivista 1981)
[3] J.V. Field e J.J. Gray, The Geometrical Work of Girard Desargues, Springer-Verlag, 1987
[4]J.P. Le Goff, Desargues et la naissance de la géométrie projective in J.Dhombres et J Sakarovitch Desargues en son temps
Libraire scientifique A. Blanchard, 1994
[5] J. Field, Linear perspective and the projective geometry of Girard Desargues , Nuncius An. Storia Sci. 2 , 1987 , pp.3-40
[6] F.Enriques, Lezioni di geometria proiettiva, Zanichelli, 1904
[7] B. Pascal, Oeuvres complètes, par J. Chevalier, 1954, Pleiade
[8]J.V Poncelet, Traité des propriétés projectives des figures, Paris, 1865
[9] Menelao, Sphaericorum, Traduzione dall'arabo in latino di Halley, Sumptibus Academicis, 1758
[10]Ptolemy, Almagest a cura di G. J. Toomer, Duckworth, 1984
[11]Fibonacci, Scritti di Leonardo Pisano, pubblicati da B. Buoncompagni, Roma, 1862
| |