|
0. Introduzione
Desargues è una figura strana e non convenzionale nell'universo scientifico del suo tempo. È vissuto nella prima parte del XVII
secolo, così fertile, in Francia, di nomi straordinari per le matematiche come Roberval, Fermat, Descartes, Pascal. In un momento in cui
la matematica stava facendo grandi balzi in avanti rispetto alla trattazione classica ereditata dalla geometria greca attraverso lo sviluppo di
nuovi strumenti algebrici, che preparavano la nascita dell'analisi, Desargues (1593-1661), e con lui il suo allievo Pascal, restò fedele
all'impostazione sintetica della geometria antica. Egli riuscì, nonostante questo, a rivoluzionare completamente il contesto euclideo e a
crearne uno nuovo, padre della moderna geometria proiettiva, tracciando una strada alternativa a quella costruita dai suoi contemporanei. Il valore
della sua opera tuttavia non fu all'epoca riconosciuto ed esaltato e si può pensare che il clamore e l'entusiasmo che creò nell'ambiente
scientifico il metodo delle coordinate di Descartes, abbia messo in ombra le teorie di Desargues. A questo si aggiunga che la sua opera principale,
il Brouillon project d'une atteinte aux evenemens des rencontres d'un cone avec un plan
1
fu stampata nel 1639 in sole 50 copie subito disperse
2
.
Molte caratteristiche del lavoro di Desargues fanno di lui un personaggio singolare, fuori dai canoni e difficile da inquadrare. Il suo stile bizzarro
e sconcertante, ha reso oggettivamente difficile la lettura dei suoi lavori, contribuendo alla lentezza della diffusione delle sue idee
Gli stessi amici di Desargues, tra i quali vanno inclusi Descartes e Mersenne che lo stimava molto e lo aveva incluso nella sua Accadémie,
che divenne in seguito l'Accadémie libre e poi, nel 1666, l'Accadémie des Sciences, avevano qualche difficoltà
ad accettare i
suoi modi. Descartes commenta così la lettura del Brouillon in una lettera del 1639 indirizzata a Desargues
3
:
Voi potete avere due propositi che sono entrambi molto buoni e lodevoli ma che non richiedono lo stesso modo di procedere: uno è di scrivere
per i dotti ed insegnar loro qualche nuova proprietà delle sezioni coniche che ancora non conoscono; e l'altro è di scrivere per
i curiosi che non sono dotti e di fare in modo che questa materia, che fino ad ora è compresa da pochissime persone e che tuttavia è
molto utile nella prospettiva e in architettura, venga divulgata e diventi di facile comprensione per tutti quelli che vorranno studiare il vostro
libro. Se voi avete il primo proposito non mi sembra sia necessario usare termini nuovi perché i dotti, avendo familiarità con quelli
di Apollonio, non li cambierebbero con facilità con altri, anche se migliori, e quindi i vostri non serviranno che a render loro
le dimostrazioni più difficili e ad allontanarli dal leggerle. Se voi avete il secondo proposito è certo che i vostri termini che sono
in francese e non mancano di spirito e di grazia, saranno accolti meglio dalle persone che non conoscono quelli antichi e anche potrebbero
attrarre molti a leggere i vostri libri [...] ma se è questa la vostra intenzione bisogna che vi decidiate a scrivere un libro molto ampio...
In effetti, accanto ad una mente acuta e geniale abitava in Desargues uno spirito pratico che lo portava a una forte tensione didattica nei
confronti di ciò che presentava al suo pubblico, spesso composto da artigiani. All'inizio della Perspective di Bosse, suo allievo e
divulgatore dei suoi scritti, troviamo riportata questa citazione, da lui attribuita a Desargues
4
:
Riconosco francamente di non aver mai provato piacere in studi o in ricerche nel campo della fisica o della geometria, se non in quanto
queste potevano servire come mezzi per arrivare a una qualche sorta di conoscenza [...] che si potesse tradurre, all'atto pratico, nel bene e
comodità della vita, che venisse usata per conservare la salute e, come applicazione, nella pratica di qualche arte, e mi sono reso conto
che una gran parte delle arti pratiche si fonda sulla geometria come su una base sicura [...] Avendo constatato l'eccellenza e la bellezza di
tali arti [la pratica del taglio delle pietre, la prospettiva, la costruzione di una meridiana], sono stato preso dal desiderio di capire, se mi
fosse stato possibile, sia i fondamenti che le regole delle loro pratiche, quali si trovano e si vedono in uso, e ho scoperto allora che coloro
che vi si dedicano ammettono di caricarsi la memoria di un gran numero di insegnamenti diversi, per ognuna di loro, che per la loro natura e
condizione producono un ingombro incredibile nella loro mente e invece di aiutarli nell'esecuzione del compito, fanno loro perdere del tempo[...]
oppure che la maggior parte dei pittori e degli altri artigiani lavorano andando alla ventura e a tentoni, senza una guida sicura, e
conseguentemente con una incertezza e una fatica inimmaginabile. Il desiderio di alleviare, se possibile, alcune di queste pene, così
faticose e spesso ingrate, mi ha spinto a cercare e a pubblicare per ciascuna di queste arti delle regole abbreviate [...], nuove, dimostrative,
più facili da capire, da apprendere e da mettere in pratica
In effetti Desargues organizzò numerosi teoremi utili agli artigiani e li divulgò tramite conferenze e fogli volanti. Sembra che egli,
nella sua missione didattica, attribuisse grande importanza alle parole tecniche in uso nelle sue opere, dal momento che si impegnò
costantemente per una loro definizione accurata, arrivando a coniarne di nuove. Nel suo stesso scritto sulla prospettiva
5
, per esempio, dedica
molto spazio alla rassegna di tutte le parole interessate, dando le definizioni e tutti i sinonimi dei nomi, nuovi o consueti, in uso nella
pratica della disciplina. Emerge da questo fatto che una parte di quella confusione a cui accennava Desargues parlando del lavoro degli
artigiani, dipendeva proprio dall'uso di termini diversi, in contesti diversi, per indicare la stessa cosa, o di significati dei termini
non ben definiti, dai contorni sfumati. Ecco allora la giusta preoccupazione, in partenza, di levare ogni ambiguità e ogni possibile
confusione in questo campo e di unificare il più possibile i termini usati.
Ma nella sua opera principale, il Brouillon, questa attenzione alle parole sembra diventare addirittura una stramberia incomprensibile
nel suo intento, generalmente di ostacolo nella lettura del testo. Egli usa termini botanici cone nodo, tronco, ramo,
ramoscello per designare
comuni oggetti geometrici come punto su una retta, retta, rette intersecantesi, segmento. Jean de Beaugrand, potente segretario del re e scienziato
oggi pressoché ignoto, scriveva nel 1640, a un anno dalla pubblicazione del Brouillon
6
...voi scuserete la libertà che mi prendo di non scusare affatto quella dell'Amico che nei Brogliacci che ha messo in circolazione, non
si è accontentato solamente di sostituire con termini barbari quelli tramandati dai sapienti, ma ha voluto anche introdurne alcuni
assolutamente ridicoli.
Tra questi includiamo il termine involution, rimasto nel linguaggio tecnico della matematica di oggi per denotare un concetto centrale
in geometria proiettiva, che Desargues introduce e concepisce con estrema chiarezza assieme alla sua invarianza rispetto alle proiezioni centrali.
Aggiunge poco dopo Beaugrand
7
Ma se non si tratta che di cogliere ciò che accade intersecando un cono con un piano, non è questo indice di uno spirito insolente?
o tanto privo della lettura di buoni libri da voler rifiutare il modo di parlare di Euclide, di Apollonio e di Archimede, per applicare male quello
di carpentieri e muratori a un oggetto la cui delicatezza ed eccellenza è infinitamente al di sopra di ciò che si chiede alle loro opere:
da parte mia, avendo letto con attenzione le prime dieci pagine del suddetto accenno, che sono esattamente un terzo di tutta l'opera, e avendo
constatato che non contenevano altro che una proposizione che è tra i lemmi di Pappo, non vi posso nascondere che mi è venuto da pensare
che Desargues abbia adottato questo modo di mal parlare in matematica, non solo perché non conosce quello giusto, ma anche perché, nel
momento in cui vengano riportate cose già esistenti altrove, si faccia più fatica a riconoscerle.[...] In verità non mi sembra
che sia riuscito in alcuno dei nomi che ha imposto, tranne che in quello di ''brogliaccio'', che ha scelto come titolo del suo libro. Potrei giurare
in tutta coscienza di non aver mai letto niente in cui vi sia meno ordine e più confusione, e che meritasse di più quel nome.
Un solo convinto apprezzamento delle idee di Desargues sembra sia stato dato da Fermat, altro grande matematico fondatore della moderna teoria dei
numeri, poco considerata a quei tempi, e la cui vicenda è per alcuni versi simile a quella di Desargues. Fermat scriveva in una lettera a
P. Mersenne datata 1 Aprile 1640
8
:
Stimo molto M. Desargues e tanto più che è lui il solo inventore delle sue coniche. Il suo libretto che dite passa per essere
scritto in gergo, mi è sembrato molto comprensibile e molto ingegnoso.
In definitiva le idee di Desargues non furono discusse a fondo negli ambienti scientifici importanti e furono invece al centro di grandi
contestazioni e polemiche nell'ambito di mediocri tecnici, che lo amareggiarono e stancarono tanto da farlo alla fine chiudere in una vita
ritirata, a Lione, lontano dalla corte e da Parigi, dedito all'insegnamento delle sue tecniche agli artigiani locali. Tutto questo ha contribuito
a fare di lui un autore in pratica sconosciuto per quasi due secoli, fino a quando Poncelet, nella prima metà del XIX secolo,
leggendo proprio i detrattori di Desargues, si rese pienamente conto dell'importanza di quelle idee. Ancora oggi Desargues è poco letto,
poco conosciuto, non esiste nessuna edizione italiana delle sue opere e quella francese curata da Taton nel 1951 è sopratutto pensata per
una ristretta cerchia di studiosi della storia della matematica. D'altra parte molti problemi di interpretazione dell'opera di Desargues restano
ancora aperti, J-P Le Goff , uno dei maggiori studiosi di questo autore, in [4] si pone il seguente ''enigma storico'': quali considerazioni hanno
portato Desargues ad introdurre un nuovo stranissimo vocabolario per denotare concetti spesso già noti, quali invece quelle che lo hanno
portato a concepire il concetto di involuzione con la sua invarianza proiettiva? Il riferimento alla pratica della pittura e della rappresentazione
prospettica alla quale allude la maggioranza dei commentatori
9
, non ci pare sufficiente. In questo lavoro cercheremo di mostrare come le
strane definizioni coniate da Desargues abbiano lo scopo di creare un nuovo ambiente concettuale, nuove immagini mentali capaci di suggerire
all'intuizione uno spazio nel quale far convivere il finito e l'infinito attuale, al fine di rimuovere gli ostacoli epistemologici derivanti
dalla classica visione euclidea del piano e dello spazio. In questo nuovo spazio la mente può imparare ad orientarsi immaginando le
figure dinamicamente nel loro processo di degenerazione quando una loro parte vada all'infinito.
Lo scopo ultimo di questa ipotetica ricostruzione è mostrare attraverso un buon esempio come sia produttivo per lo sviluppo delle idee
matematiche, qualunque sia il livello, da quello delle scuole elementari alle più avanzate ricerche scientifiche, il poter accompagnare
il ragionamento logico-deduttivo con produttive immagini mentali facendo interagire in modo costruttivo il pensiero sintetico con quello analitico.
1. Il seme della trasformazione
L'esplorazione del mondo fisico avviene nell'uomo essenzialmente attraverso la vista e attraverso il movimento e il tatto. La nostra mente si
affida a due rappresentazioni incongrue tra loro e vi si muove agilmente, traendone conclusioni e inferenze giuste, nonostante le informazioni
contrastanti che arrivano dai nostri sensi. Il tatto ci dice che un rettangolo resta uguale a sé in qualunque occasione avvenga l'esplorazione,
mentre lo stesso oggetto è visto in molti modi diversi, se ci spostiamo. Le forme che si generano nella visione in movimento di un oggetto
mantengono tuttavia, nel loro variare, una forte invarianza ontologica che le unifica cognitivamente tra loro. Guardando un cerchio da una
posizione non frontale, per esempio, continuiamo a riconoscerlo come un cerchio, anche se ci appare come un'ellisse.
La rappresentazione percettiva e cognitiva del mondo fisico quindi si svolge su due piani che continuamente si integrano: quella del mondo
dell' ''essere'' e quella del mondo dell'''apparire''.
Nello sviluppo del pensiero scientifico le proprietà metriche del mondo dell'essere hanno portato alla splendida costruzione
della geometria euclidea. L'indagine dei rapporti tra gli oggetti studiati permette di definire logicamente alcuni di tali oggetti
per mezzo di altri - ad esempio il triangolo può essere definito tramite la retta e il punto a partire da elementi primitivi
che non hanno la possibilità di essere definiti in tal modo senza causare circoli logici viziosi. Nella geometria euclidea questi
elementi fondanti, il punto, la retta e il piano, sono nati rispettando fortemente le proprietà intuitive che ci arrivano
dall'immersione nel mondo reale. In essa poi le forti proprietà metriche rendono regina la forma, statico oggetto di contemplazione
platonica, attorno alla quale l'indagare si snoda attraverso ampliamenti, sottrazioni, ricentramenti, ma mai con trasformazioni che
colleghino forme tra loro. L'unica occasione che vede l'introduzione di un movimento è creata dalla necessità di definire
uguali due oggetti geometrici. Notoriamente Euclide, con qualche disagio concettuale, si affida per questo a una sorta di intuitivo
movimento meccanico di trasporto, nel quale due oggetti si identificano quando, se sovrapposti, coincidono.
La geometria del mondo ''come si vede'' ha avuto una sorte diversa e legata più alle arti pratiche che alle discipline nobili della
matematica, ma ha comunque prodotto teorie rigorose nel loro impianto assiomatico. Un esempio in questo senso è dato dall'Ottica di Euclide,
che si pensa fosse impiegata all'epoca come guida nelle costruzioni scenografiche delle rappresentazioni teatrali e delle opere artistiche e
architettoniche in genere. Gli assiomi dell'Ottica rendono possibile trattare e prevedere in modo rigoroso le trasformazioni subite dalla forma
e dalle dimensioni apparenti di un oggetto in funzione delle variazioni del punto di vista.
Anche i metodi prospettici perfezionati nel rinascimento hanno impegnato i matematici, che hanno corretto i principi approssimativi che venivano
applicati dagli artigiani come puri espedienti pratici nell'esecuzione delle loro opere e ne hanno dato dimostrazioni rigorose all'interno della
geometria classica. Il loro concentrarsi sulle figure geometriche da un punto di vista prospettico ne ha esaltato le proprietà grafiche
e ne ha indotto una forte separazione da quelle metriche, portando così a una concezione più generale delle figura stesse.
Con la prospettiva si insinua in geometria il concetto di trasformazione, che passa, senza essere formalmente definito, attraverso nuovi termini,
quali il ''degradare'', coniati da matematici e pittori come Piero della Francesca. Nell'accezione di Piero un oggetto degradato è il
trasformato di un oggetto reale sul piano del quadro e il degradare è l'operazione mediante la quale, attraverso procedimenti geometricamente
corretti, si attua graficamente la proiezione, arrivando al giusto disegno prospettico.
Questo primitivo concetto di trasformazione di forme pervade la concezione geometrica di Desargues e lo porta con forza a studiare la proiezione
di una configurazione in un'altra, arrivando a vedere tale proiezione, modernamente, non solo come collegamento puntuale tra forme ma anche
tra le intere superfici che le contengono. La ricerca dell'unificazione delle coniche condurrà Desargues a proporre la ''innaturale'' ma
risolutiva identificazione dei due versi di una direzione in un unico punto all'infinito. Si rende in questo modo impraticabile all'immaginazione
il contesto totale cercato, ma si soddisfa l'esigenza matematica di mantenere una necessaria continuità alla trasformazione.
Non sappiamo nulla sul contenuto delle sue Leçons de tenebres, che pare tenesse dopo il suo ritiro a Lione, tranne questa testimonianza riportata
in una lettera
10
di Oldenburg a Leibniz, del 1673, dalla quale emerge la grande modernità con la quale Desargues tenta di costruire un modello
topologico del piano proiettivo:
Abbiamo avuto recentemente sotto gli occhi, per un esame, un trattato di prospettiva in-folio, scritto da Huret, nel quale lui critica e rigetta
le coniche di Desargues intitolate Leçons de tenebres, di cui abbiamo sentito dire sono state stampate solo 50 copie in tutto di difficile
reperimento; se l'intenzione dell'autore è bene interpretata la dottrina merita lodee va sviluppata piuttosto che biasimata. Ora il suo
progetto era di trattare le sezioni coniche come proprietà di cerchi più piccoli situati sulla superficie di una sfera; per
spiegare questo si suppone che l'occhio sia al centro della sfera, la quale sia toccata da un piano sul suo Zenit e che si percepisca
il piano attraverso la sfera, il detto piano è la base d'un cono il cui vertice è l'occhio: se un cerchio è al di sopra
dell'orizzonte e se è anche un parallelo, la sezione sul piano tangente è un cerchio, ma se non è un parallelo è
una ellisse, e se tocca l'orizzonte ma tutte le altre parti del cerchio sono sopra l'orizzonte, è una parabola e guardando diversi
cerchi elevarsi in modo da toccare l'orizzonte in uno stesso punto, la loro proiezione condurrà a parabole tutte congruenti; ma se
un cerchio o più cerchi si trovano parte al di sotto e parte al di sopra dell'orizzonte, le loro proiezioni sono delle iperboli e
se questi cerchi hanno una corda comune sull'orizzonte le loro proiezioni sono delle iperboli congruenti; se questi cerchi sono interamente
sotto l'orizzonte non si possono proprio proiettare.
Questa nota riporta un esempio che aiuta a concepire la grande innovazione di Desargues: le coniche erano classicamente studiate,
fin dall'antichità, come sezioni di un doppio cono retto. Le forme, ancora platoniche come concezione, determinate dal piano secante
sulla superficie del cono erano via via definite come cerchio, o ellisse, o parabola.., e il tentativo di unificare il loro studio in un'unica
trattazione non aveva avuto che uno sbocco algebrico.
La proiezione di una semisfera su un piano, così chiaramente descritta, ci porta invece a considerare le coniche come ''trasformazioni''
visive (proiettive) di una circonferenza da una semisfera su un piano, introducendo nella geometria sintetica il seme del concetto di
corrispondenza.
L'immaginare la volta celeste e la sua proiezione dal centro sul piano tangente alla sfera nello Zenit, porta a identificare cognitivamente,
attraverso il punto di vista, l'infinito con l'orizzonte e le coniche con cerchi che intersecano diversamente l'orizzonte. Se questa immagine,
per lo meno localmente
11
, può aiutare la nostra intuizione, nello stesso tempo essa porta a modificare completamente la struttura classica
dello spazio intervenendo sul concetto di parallelismo e di infinito su cui è fondato l'intero edificio euclideo.
2. Le immagini dell'infinito
Il Brogliaccio di Desargues ha la caratteristica di non essere, come bozza, canonicamente formalizzato e pare quasi possa farci rivivere l'atto
creativo nel momento in cui prende forma. Le immagini che Desargues costruisce attraverso i nuovi, strani termini introdotti, vogliono creare,
crediamo, una comprensione più profonda del nuovo mondo geometrico che lui è riuscito a concepire.
Dal punto di vista dell'immaginazione, ogni costruzione euclidea avviene ''al finito'' e per questo il ''lontano'' e il ''vicino'' sono semplici
prolungamenti o contrazioni di mappe locali. Le rette in Euclide sono segmenti che possono essere prolungati a piacere, dando luogo ad altri
segmenti. Le figure sono chiuse e limitate e qualunque dilatazione o contrazione resta nell'ambito della similitudine, rendendo possibile
ricostruire attraverso un'immagine le proprietà ricavate con procedimenti logico deduttivi. Desargues invece si spinge oltre, cercando di
immaginare come le figure possano coerentemente collocarsi e distendersi in uno spazio contenente il proprio infinito e in questo tentativo vede
con chiarezza le difficoltà a conciliare l'intuizione col ragionamento, costretti entrambi da preesistenti e consolidati schemi
euclidei.
Ad esempio, volendo descrivere la figura che si ottiene intersecando un cono con un piano non passante per il vertice e non parallelo alle
generatrici, osserva che, mentre al finito questa figura è semplicemente una ellisse
12
se questa intersezione è a distanza infinita l'evento è inimmaginabile e l'intuizione è troppo debole per capire come
può accadere quello che il ragionamento le fa concludere.
Nello spazio che Desargues intuisce, l'infinito è un'estensione in atto, che rompe vecchi schemi concettuali nei quali, come per
i numeri, l'infinito esprime solo la possibilità di crescere a piacere. La difficoltà ad immaginare e poi descrivere tale spazio
costituisce una sfida che lui affronta, ed è anche per questo, non solo per i risultati sulle teoria delle coniche sorti dal nuovo contesto,
che la sua opera è significativa. Dice all'inizio del Brouillon per presentare la materia del suo lavoro
13
:
Ciascuno penserà quello che gli sembrerà più opportuno di ciò che qua deduciamo e della maniera di dedurlo e vedrà
come la ragione cerchi di comprendere sia le grandezze infinite che quelle così piccole da avere le opposte estremità unite tra loro e
vedrà come il pensiero si perda anche perché sarà portato, attraverso il ragionamento ordinario, ad accettare delle
proprietà delle quali è incapace di capire come possano essere.
Certo la pratica del disegno prospettico, della quale Desargues era un ottimo conoscitore, ha contribuito a sviluppare in lui una forte intuizione
dell'infinito spaziale. Se guardiamo due rette parallele allontanarsi da noi lungo un data direzione esse si vedono convergere verso un ''punto
infinitamente lontano'' che nella rappresentazione prospettica viene disegnato con un punto effettivo posto sulla linea dell'orizzonte. Ma se ora
ci giriamo e guardiamo le due rette parallele nell'altro verso ancora le vediamo unirsi in un punto, ma le vediamo unirsi in un altro quadro
che è quello che ora abbiamo davanti a noi. Questi due quadri, queste due rappresentazioni, quella davanti e quella dietro come si
amalgamano nel nostro pensiero dando luogo a un'immagine coerente? Ci sono due punti infinitamente lontani dove le rette parallele s'incontrano,
uno da una parte e uno dall'altra, o ne esiste uno solo? E l'orizzonte che vediamo come una linea retta, e così lo vediamo anche quando ci
giriamo, come possiamo rappresentarcelo globalmente? Se ogni retta ha una direzione qual'è la direzione dell'infinito? E' forse pensabile
come una circonferenza? Ma in questo caso cosa c'è fuori dalla circonferenza? E' possibile andare oltre l'infinito? E' possibile scavalcare
l'orizzonte? Ma se questo non è possibile a che cosa corrisponde quello spazio che pure vediamo sul nostro quadro e che sta sopra
l'orizzonte? Cosa rappresenta quell'altrove?
Come si vede la mente si sente vagare, l'immaginazione si perde e il ragionamento cerca di guidare entrambe. Siamo di fronte ad un interessantissimo
caso in cui la nostra intuizione spaziale non riesce spontaneamente a trovare risposte coerenti all'interno del suo sistema di connessioni e,
in un qualche modo, chiede aiuto al pensiero logico deduttivo. Vediamo l'infinito nei vari quadri dove vediamo rispecchiarsi lo spazio, ma non
riusciamo a ''incollare'' coerentemente i dati locali, forniti dalle varie rappresentazioni e immaginare uno spazio globale. Occorrono dunque
nuovi strumenti capaci di guidare il pensiero verso la comprensione di questi fatti
14
.
Siamo convinti che Desargues non solo si rendesse pienamente conto di questa difficoltà ma cercasse in ogni modo di costruire dei modelli
geometrici capaci di guidare l'intuizione. Egli sembra rendersi conto della difficoltà di descrivere questo nuovo spazio dove
l'entendement s'y perd, ma accetta la sfida e, per guidare la propria e l'altrui intuizione, inventa nuovi termini, un nuovo mondo
geometrico fatto di traguardi, di alberi, di nodi, di rami e ramoscelli, di involuzioni, che aiutino a modificare l'immagine cristallizzata
di uno spazio euclideo nel quale le figure vivono prigioniere di una scatola e possono essere sì prolungate quanto si vuole, ma non
raggiungono comunque mai l'infinito. E invece ora che l'infinito è stato raggiunto è proprio in rapporto ad esso che nasce una
nuova geometria delle figure: l'infinito diventa parte significativa dello spazio e le figure rispetto ad esso prendono forma. L'iperbole è
la sezione di un cono la quelle à distance infinie se mipartit en deux moitiez opposées dos à dos , mentre la parabola
à distance infinie rentre et repasse en soy mesme
15
.
La difficoltà che incontra il pensiero nell'intuire e immaginare questo nuovo ambiente e la resistenza a cambiarne la fisionomia
rispetto a quello euclideo, è in parte dovuta al fatto che i due enti fondanti, la retta e il punto, sono ancora cognitivamente legati
alla primitiva e intima concezione di essi, coincidente con quella formatasi ''per immersione'' nella vita reale e consolidata nella cognizione
con lo studio della geometria euclidea, quasi fossero enti ''assoluti''. La piena ripresa dell'attività intuitiva avverrà solo
quando l'esperienza immaginativa avrà pazientemente costruito un sufficiente numero di figure strettamente legate ai nuovi assiomi, alle
nuove istruzioni verbali, senza caricarle di elementi impropri, ad esse estranee, e avrà di fatto reso queste rappresentazioni fondamenta
per una nuova base concettuale, che possa guidare produttivamente le simulazioni necessarie allo sviluppo delle idee.
Noi riteniamo che il nuovo linguaggio che Desargues propone nasconda il tentativo da parte sua di mettere il lettore in una nuova ottica mentale,
che gli permetta di staccarsi un po' alla volta dal contesto euclideo per avventurarsi in un campo nel quale la mente trova molte difficoltà,
legate non alla razionalità, ma alla rappresentazione intuitiva di un nuovo mondo geometrico.
Il modo in cui Desargues inizia il Brouillon spazza via ogni interpretazione che vede nei neologismi che verranno usati solo un inutile e fastidioso
vezzo dell'autore, e ci mostra subito la questione da lui individuata, collegata al testo da leggere
16
:
Non sarà qui difficile fare la necessaria distinzione tra le assegnazioni di un nome, cioè le definizioni, le proposizioni,
le dimostrazioni, là dove seguono, dalle altri parti del discorso, e neanche [fare distinzione] tra lo scegliere fra le figure, quella
appropriata al testo che si sta leggendo, oppure il costruire le figure sulle indicazioni delle frasi scritte.
Desargues allarga la questione: non è solo un problema linguistico ma anche un problema di immagini: la giusta comprensione del ruolo
di un termine all'interno del discorso matematico è importante quanto il saper distinguere tra l'opportunità di choisir, in un
insieme di figure consuete, quella appropriata al periodo che si sta leggendo e la necessità di faire nuove figure seguendo fedelmente
l'indicazione dei termini usati nel discorso, liberandole in tal modo da fissità funzionali e implicazioni parassite legate a vecchi
contesti.
Lo sconcerto di avere qualche volta gli occhi della mente al buio non è l'unico che assale il lettore del Brouillon. Gli si chiede di muoversi
in un contesto geometrico nel quale le consuete stabilità di forma e di proprietà si rompono e l'indagine si srotola su sentieri nei
quali la deformazione per proiezione è sempre presente, imponendo una nuova ricerca di punti stabili e di proprietà invarianti.
L'intuizione deve abbandonare la statica contemplazione di figure euclidee per acquisire un abito dinamico che consiste nel modificare continuamente
le forme, nel degenerarle col pensiero, nel portare all'infinito alcune loro parti cercando di intuirne la sorte. Le proiezioni centrali sono, per
questo scopo strumento di estrema utilità, permettendo di trasferire proprietà proiettive invarianti da una figura, per la quale sia
più facile dimostrarle, a un'altra ottenuta come sua proiezione (ad esempio da un cerchio a una conica) ricavando per questa via nuovi
risultati. Questo è quello che giustamente Taton
17
descrive come la prima chiara presenza della prospettiva come metodo di dimostrazione
geometrica, un modo di ragionare, che è stato ripreso con grande successo a partire dal XIX secolo dai maggiori geometri ed è usato
ancora ai giorni nostri. Lo stesso Desargues ben cosciente della novità, fornisce, come vedremo meglio, una dimostrazione formalmente
ineccepibile del suo celebre teorema del rameto, così chiamato con un'espressione felice da D. Bessot, ottenuta considerando una lunga
catena di rapporti composti, ma nel contempo ne suggerisce un'altra fortemente intuitiva basata sulla degenerazione di un quadrangolo e delle
sue diagonali a un punto!
2. Il giardino di Desargues
Leggiamo nella biografia di Desargues che era proprietario di una casa di campagna a Condrieu nella quale andava spesso, e che amava curare
personalmente il suo giardino. Non possiamo sapere ovviamente se l'inclinazione per questo ambiente naturale lo abbia influenzato nella scelta
delle parole da usare nella sua opera, ma pensiamo che molte di esse abbiano un carattere metaforico indovinato, che induce ad opportune analogie e a trasferire su una nuova struttura, in via di definizione, caratteristiche e configurazioni appartenenti a strutture conosciute, appositamente scelte.
Fin dall'inizio, nel considerare gli elementi primi della geometria, la retta e il punto, troviamo in Desargues un atteggiamento nuovo ed
emblematico
18
:
Qua ogni linea retta è pensata allungata al bisogno all'infinito da una parte e dall'altra.
La retta è di fatto allungata all'infinito e non potenzialmente allungabile. Questo oggetto, con l'invito ad andare col pensiero all'infinito,
si presenta fin dall'inizio diverso dalla retta - segmento euclideo e la differenza diventa ancora più chiara subito dopo, quando Desargues
introduce i fasci di rette (ordonnance des lignes droictes), e chiama but
19
la ''meta'', il ''punto'' che le rette del fascio hanno in comune.
Questo termine conferisce a quel particolare ''punto'' un significato profondo, che lo circonda di possibili movimenti e associazioni di
pensiero: questo ''punto'' diventa meta comune cui le rette tendono, una caratteristica che le lega insieme in un unico destino, una sorta di
comune inclinazione verso un ''dove'' che può essere a distanza finita o a distanza infinita. L'immagine mentale che il termine but
suggerisce ha la tensione che il termine stesso vuole esprimere:

Immagine 1
ed è ben diversa dall'immagine che avremmo se Desargues avesse dato una definizione formale di fascio di rette, in termini di
''punto comune a tutte le rette del fascio''. Il termine ''punto'' infatti richiama il classico bagaglio concettuale geometrico e l'immagine
che ne risulta appare molto impoverita:
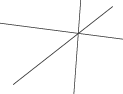
la tensione dell'immagine precedente, che ammetteva anche l'infinito, si è persa. La parola but al posto della parola punto suggerisce
una stessa ontologia nel caso che il but sia a distanza finita o infinita, e quel che più conta contiene implicitamente un nuovo
fondamentale
principio, che diventerà il primo postulato della geometria proiettiva: due rette in uno stesso piano hanno sempre un but comune
20
.
Immaginare la retta come un'estensione in atto con un solo punto all'infinito e non come un possibile tendere verso l'infinito, mette in secondo
piano il concetto di ''verso'' esaltando nel contempo quello di ''direzione''
21
. Desargues sceglie dunque di assegnare un solo punto all'infinito
comune a due rette parallele. La scelta di questo principio è particolarmente felice perché in questo modo la corrispondenza tra i
punti di due rette o di due piani proiettivi che si ottiene tramite una proiezione centrale diventa biunivoca. Ci sono anche ragioni di
continuità suggerite dalla visione dinamica di Desargues, che spingono la mente ad immaginare la retta con un but, una meta
all'infinito
che unisce tra loro le due estremità opposte della retta
22
.
Passiamo in rassegna alcune delle nuove definizioni che vengono introdotte all'inizio del Brouillon nel tentativo, a nostro avviso ben riuscito,
di creare nuove immagini mentali capaci di sviluppare una intuizione dinamica protesa verso un altro ambiente geometrico.
Tronc (tronco): si chiama tronco una retta quando per un certo numero dei suoi punti passano altre rette.
Neud (nodo): si chiama nodo ogni punto del tronco per il quale passa una retta.
Rameau (ramo): la retta che passa per un nodo del tronco si chiama ramo.
Rameau déployé au tronc (ramo dispiegato dal tronco): è una retta che interseca il tronco senza coincidere con esso.
Rameau plié au tronc (ramo piegato sul tronco): è un qualunque segmento del tronco racchiuso tra due nodi.
Brin de rameau (ramoscello): è un qualunque segmento di ramo contenuto tra il suo nodo e un altro ramo.
Seguendo queste indicazioni, si assiste alla costruzione di un mondo matematico al centro del quale sta un tronco. La definizione di
tronco è prettamente matematica: si chiama tronco una retta per qualche punto della quale passino altre rette. Ma l'uso della parola
non tecnica guida immediatamente la costruzione dell'immagine associata: il tronco diventa la struttura principale, portante, e i suoi rami
si intrecciano tra di loro partendo dai nodi su di esso. In questa struttura gli elementi focali della figura sono costituiti dal tronco, dai
nodi e dal movimento dei rami rispetto al tronco immobile: il loro piegarsi e dispiegarsi da esso. La natura sempre non finita del ramo poi
abitua l'occhio e la mente a non restringere il campo della figura in una forma limitata, ma a tenere sempre presente il suo effettivo
estendersi all'infinito, dato dalla possibilità del punto di intersezione di due rette di essere o non essere a distanza finita. Passano
completamente in secondo piano, anche se appaiono chiaramente, elementi classici euclidei come i triangoli.
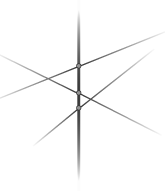
Immagine 2
Altro elemento importante è il ramoscello: è una qualunque porzione di ramo che sia compresa tra il suo nodo e
l'intersezione con un altro ramo. I segmenti, in questa rappresentazione, hanno dignità solo se hanno almeno un estremo su
un nodo del tronco.
Per esempio, nel caso seguente
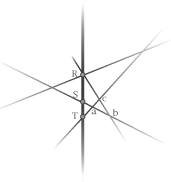
Immagine 3
i segmenti ab, bc, ac, non hanno un nome che li definisca tramite la loro relazione col tronco, come invece accade per i getti
Rc, Rb, Sa, Ta, e quindi non hanno neanche dignità di oggetti, e con loro neanche il triangolo abc. L'occhio del matematico,
veloce nell'individuare tutte le possibili forme euclidee contenute in una raffigurazione, anche le più nascoste, deve abituarsi
a ''ragionare'' visivamente basandosi principalmente sui nodi, sui rami e sui ramoscelli, con la loro possibilità di chiudersi o
di aprirsi sul tronco.
Anche questa volta, come nel caso del calcolo formale di complicati rapporti nella Perspective
23
Desargues trova un espediente
per costruire una gestalt privilegiata, una forma pilota che guiderà dinamicamente gran parte delle dimostrazioni dei teoremi nel
suo lavoro sulle coniche, e riteniamo che anche per questo scopo abbia mantenuto nella sua creazione la forza dell'alone metaforico dei
suoi termini.
3. Alberi, ceppi e involuzioni
L'immagine del tronco perde la sua genericità e diventa il caso particolare di albero quando nel tronco si individua una origine:
''il ceppo'' e una particolare configurazione di rami e di nodi.
Un arbre (albero) è un tronco con une souche (un ceppo) O e varie branches couplées (getti accoppiati o coniugati) tra
loro che nascono dal ceppo e si sovrappongono al tronco.

Immagine 4
Immagine animata
Se OA e OA' sono due tali getti accoppiati, si richiede che il prodotto OAXOA', col segno che gli compete
24
, abbia un valore costante
non nullo.
La struttura ad albero permette di stabilire una corrispondenza biunivoca (e involutoria) tra i nodi del suo tronco nel senso che al nodo A
resta associato in modo unico un nodo A', a B un nodo B' ecc e, viceversa, ad A' è associato A, a B' è associato B ecc. Gli
accoppiamenti sono fatti in modo tale che l'area del rettangolo che ha per lati due ramificazioni accoppiate non cambi:
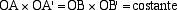
Si vede anche come, avvicinando B al ceppo O il suo corrispondente B' degenera all'infinito e in questo caso la relazione precedente degenera
nella ardita formula:
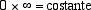
Un albero sarà dunque definito da un tronco, un ceppo e una costante (positiva o negativa) con la quale accoppiare i getti.
Il primo risultato importante di Desargues è quello di rendere la struttura involutoria di tali nodi indipendenti dal ceppo,
dandone una caratterizzazione intrinseca
25
:
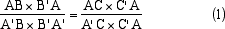
relazione quest'ultima che non coinvolge il ceppo O
26
.
La speciale configurazione data da tre coppie di punti disposte su un tronco in modo da appartenere ad uno stesso albero come coppie coniugate,
viene chiamata da Desargues involuzione e la relazione precedente, la (1), ne fornisce una caratterizzazione quantitativa. E' un concetto
questo riposto e molto profondo, invariante per trasformazioni proiettive, strumento centrale nel metodo di Desargues. E' ancora l'occhio
del pittore che, nello stesso modo in cui proietta le tre dimensioni dello spazio nelle due della sua pittura, proietta ora una configurazione
a due dimensioni sull'unica dimensione del tronco. Le involuzioni, in questo modo, si legano ad elementi grafici (formati cioè da
configurazioni di rette e punti) che, come tali, sono invarianti per proiezioni centrali. Nasce così la geometria proiettiva.
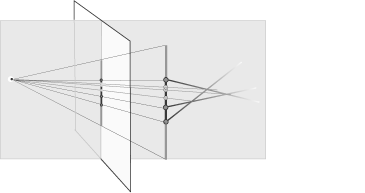
Immagine 5
Immagine animata
È possibile raffigurarci le involuzioni nello spirito intuitivo di Desargues? È possibile creare attorno a loro una dinamica
in grado di produrre, attraverso il ragionamento, nuovi teoremi geometrici, nuove e più profonde intuizioni? E' quanto cercheremo
di fare nella seconda parte di questo lavoro lasciandoci condurre nel giardino di Desargues dalle metafore che lui sembra suggerirci.
Bibliografia
[1] N. Poudra, Oeuvres de Desargues réunies et analysées, 2 Volumi , Paris, 1864
[2] R. Taton, L'oeuvre mathématique de G. Desargues, Presses Universitaires de France, 1951 (seconda edizione rivista 1981)
[3] J.V. Field e J.J. Gray, The Geometrical Work of Girard Desargues, Springer-Verlag, 1987
[4]J.P. Le Goff, Desargues et la naissance de la géométrie projective in J.Dhombres et J Sakarovitch Desargues en son temps
Libraire scientifique A. Blanchard, 1994
[5] J. Field, Linear perspective and the projective geometry of Girard Desargues , Nuncius An. Storia Sci. 2 , 1987 , pp.3-40
[6] F.Enriques, Lezioni di geometria proiettiva, Zanichelli, 1904
[7] B. Pascal, Oeuvres complètes, par J. Chevalier, 1954, Pleiade
[8]J.V Poncelet, Traité des propriétés projectives des figures, Paris, 1865
[9] Menelao, Sphaericorum, Traduzione dall'arabo in latino di Halley, Sumptibus Academicis, 1758
[10]Ptolemy, Almagest a cura di G. J. Toomer, Duckworth, 1984
[11]Fibonacci, Scritti di Leonardo Pisano, pubblicati da B. Buoncompagni, Roma, 1862
| |