L'ombra della cupola
Piero della Francesca e il Rinascimento scientifico

di Franco Ghione

Io solea maravigliarmi insieme e dolermi
che tante ottime e divine arti e scienze,
quali per loro opere e per le istorie veggiamo copiose
erano in que' vertuosissimi passati antiqui,
ora così siano mancate e quasi in tutto perdute:
pittori, scultori, architetti, musici, ieometri, retorici,
auguri e simili nobilissimi e maravigliosi intelletti oggi
si truovano rarissimi e poco da lodarli.

L.B. Alberti , De Pictura

 



Grandi cose e grandi pensieri scuotevano le menti libere di quel gruppetto di intelluttuali, artisti - scienziati, che nel '400 avrebbero riempito coi loro lavori i musei del mondo e dato la gioia ai secoli a venire di rivedere in quello una rinascita dell'Umanità. La ricoperta dei classici greci e latini nel ridare al pensiero la sua natura laica e creativa, svincolandolo dal peso della divinità rivelata, riusciva a diffondere in quel gruppo, come una epidemia, la voglia di capire, di scoprire, di realizzare opere straordinarie. Queste potevano nascere solo all'interno di un pensiero scientifico e da una ricerca del bello e della misura, tutta umana come lo era quella di Euclide o Socrate o Fidia. Quando Alberti vide il modo e la grandiosità con cui Filippo Brunelleschi stava alzando a Firenze, con ogni sorta di nuovi macchinari, la cupola di Santa Maria del Fiore scrisse 1 :

vedendo qui struttura sì grande, erta sopra e' cieli, ampla da coprire con sua ombra tutti e' popoli toscani, fatta sanza alcuno aiuto di travamenti o di copia di legname, quale artificio certo, se io ben iudico, come a questi tempi era incredibile potersi, così forse appresso gli antichi fu non saputo né conosciuto?

Così Alberti ebbe modo di esprimere la sua meraviglia col dubbio, che pervaderà questo intervento, che tutto questo e molto altro fosse già saputo dagli antichi e dimenticato, distrutto dalla violenza delle guerre e dalla barbarie del conquistatore. Anche la pittura, affine e certo indispensabile all'architettura, produceva, per la perfezione degli scorci prospettici che era possibile realizzare, dei ''miracoli''. 2

dimostrazioni quali, fatte da noi, gli amici, veggendole e maravigliandosi, chiamavano miracoli.

Pare, secondo la testimonianza di Manetti (entusiasta discepolo di Brunelleschi) che la prospettiva sia nata da una burla. Non interessa quà sostenere o meno la veridicità di questa storia quanto farla nostra per aiutare il nostro pensiero, oggi immerso in ogni tipo di immagine, a capire il senso straordinario di quei ''miracoli''. Pare che Brunelleschi avesse costruito e dipinto due tavolette che rappresentavano in perfetta prospettiva la Piazza della Signoria col palazzo Ducale ma che andavano viste ponendo l'occhio dietro la tavoletta in un piccolo foro in modo che l'immagine dipinta fosse vista riflessa da uno specchio tenuto di fronte col braccio teso. Questo marchingegno che forzava l'occhio dell'osservatore in una determinata posizione e il disegno riflesso sullo specchio a una distanza fissa, unito al fatto che il cielo, colorato in argento, rispecchiava il movimento reale delle nuvole, dava l'illusione, in qualunque luogo si fosse, di vedere la piazza. La burla, e altre se ne raccontano intorno alla figura straordinaria di Brunelleschi, consisteva nel fatto di costruire una realtà fitizzia così corrispondente ai meccanismi di ricomposizione della realtà del nostro pensiero da creare l'illusione emotiva di essere in quella realtà ricreata. Si veniva così a rompere il vecchio confine tra il possibile e l'impossibile e Leonardo, per citare solo un esempio, riusciva, col suo Cenacolo, a ''fotografare'' a distanza di secoli e secoli il Cristo con gli apostoli dando l'impressione mistica a chiunque veda il dipinto di essere in quella stanza e di vivere quel momento. Questi ''miracoli'' erano conseguenze di una scienza, di un nuovo pensiero geometrico, che molti hanno creduto e credono figlio del Rinascimento, capace di codificare in modo preciso e non empirico la geometria della visione, con lo scopo di creare un'equivalenza tra la visione di un quadro e quella della realtà restituendo, nelle due dimensioni del dipinto, la tridimensionalità della scena. Non che questo problema fosse assente dalle botteghe d'arte dei grandi maestri del '200 e del '300, anzi era forse questo uno dei problemi più difficili e di maggior interesse: ogni maestro dava una propria soluzione, spesso diversa da quadro a quadro, formulando delle regole soggettive, senza alcuna motivazione se non di natura estetica e visiva.


L'occhio non basta

Per dare un'idea seppur vaga di questi primi tentativi di dare una soluzione geometrica al problema di come rappresentare la profondità riferiamo di due metodi entrambi sbagliati in voga nelle bottghe d'arte prerinascimentali.
Per cominciare si trattava di decidere come rappresentare sul dipinto un pavimento squadrato con linee di profondità che si allontanano verso l'orizzonte, e linee trasverse a loro perpendicolari e parallele al piano del dipinto. Tale pavimentazione permetteva, una volta realizzato lo scorcio, di ''squadrare la profondità'' e di collocare conseguentemente i personaggi e gli oggetti da rappresentare nella giusta posizione prospettica. Ora, per quel che riguarda le linee di profondità, una qualche esperienza diffusa dall'osservazione di strade o filari di alberi suggeriva di rappresentarle nel quadro come se fossero convergenti a un particolare punto che Alberti chiamerà ''punto centrico'', ma per le linee trasverse che si vedono avvicinarsi tra loro man mano che si allontano verso l'orizzonte, pur essendo nella realtà della pavimentazione equidistanti, mancava una qualche evidenza coerente con la visione. Per questo le varie botteghe d'arte suggerivano metodi diversi, spesso tenuti segreti che potevano dunque essere apprersi solo attraverso la frequentazione orale del maestro il cui prestigio dipendeva naturalmente dalla sapienza di quella che Luca Pacioli chiamava segretissima scienza 3 . Uno di questi metodi è il così detto metodo delle superbipartienti che Alberti critica aspramente 4 . Superbipartiente è un termine della matematica e della musica medioevale e indica un rapporto proporzionale di due terzi, più esattamente indica la diminuzione di un terzo di una delle due quantità. La proporzione che passa ad esempio tra 9, 6 o tra 6 e 4 (diminuzione di un terzo) veniva chiamata "superbipartiente". Il metodo consiste nel dividere la linea di terra in un certo numero di parti uguali, di fissare il punto centrico C, di scegliere la prima alzata AP ad occhio e tracciare le altre nella proporzione superbipartiente, cioè diminuendo via via di un terzo la quantità trovata.


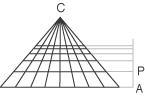
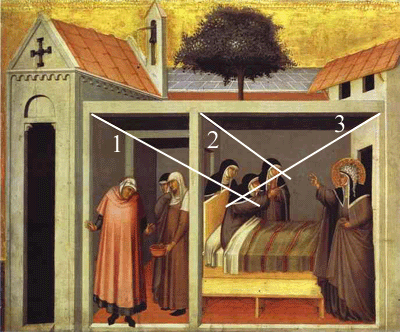
Il risultato sembra realizzare, a occhio, un buono scorcio della pavimentazione. Sembra che l'Annunciazione di Ambrogio Lorenzetti (1344) dove Maria siede su un pavimento squadrato, sia stato realizzato secondo questo metodo.


Alcuni studi di Pisanello 5 confermano, anche dal punto di vista numerico, l'uso frequente di questa tecnica ancore nel XIV secolo.
Un altro metodo, molto curioso, per realizzare lo scorcio di una pavimentazione regolare, ci viene descritto da Ignazio Danti 6 . Si fissa, come al solito, il punto centrico C e si divide la linea di base in un certo numero di parti. Si traccia poi un quarto di circonferenza, come nella figura seguente, e si divide l'arco in un certo numero di parti uguali (si suggerisce di dividerlo in 15 parti uguali), si congiungono queste parti col punto A e si tracciano le parallele alla linea di base che corrisponderebbero alle immagini prospettiche delle linee trasverse


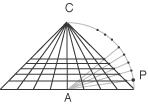
Anche in questo caso il risultato non sembra lontano dall'effetto prodotto dalla visione di un pavimento orizzontale. Tuttavia questi metodi erano approssimativi, geometricamente sbagliati. Sarà Alberti a criticarli apertamente nel De Pictura poco prima di suggerire il suo ''modo ottimo''.
Ma cosa vuol dire che un metodo è ''geometricamente sbagliato''? Come si puņ scegliere una procedura rispetto ad un'altra se non con criteri estetici? E' nel tentativo di rispondere a queste domande che avviene un salto di pensiero, una svolta di grande portata.


Verso un modello scientifico

Sia Alberti che Leonardo che Piero della Francesca che per primi hanno scritto sulla prospettiva, cercano una risposta nei metodi della geometria. Scriverà Leonardo:

... quelli che si innamorano della pratica senza scientia sono come nocchieri che entrano in naviglio senza timone o bussola, che mai hanno certezza dove si vadano. Sempre la pratica deve essere edificata sopra la buona teoria, della quale la prospettiva è guida e porta e senza questa nulla si fa bene.

E Piero della Francesca 7 parlerà di prospettiva come di vera scientia. La riscoperta della cultura classica, e in particolare di quella scientifica, ha ovviamente un ruolo centrale in questa svolta. Euclide e i suoi Elementi, variamente tradotti e commentati, diventeranno un paradigma di rigore e metodologia scientifica, un modello a cui riferirsi. Tuttavia lo spunto che permette di costruire la prospettiva su basi geometriche nasce, crediamo, più che da una consapevole metodologia scientifica, basata su postulati e definizioni iniziali, dalla forza di una metafora largamente diffusa negli ambienti intellettuali dell'epoca: la metafora del vetro. Scrive Alberti 8 :

...in questa superficia si representino le forme delle cose vedute, non altrimenti che se essa fusse di vetro tralucente tale che la pirramide visiva indi trapassasse, posto una certa distanza, con certi lumi e certa posizione di centro in aere e ne' suoi luoghi altrove.

 e ugualmente Leonardo da Vinci con un disegno e una frase sintetizza lo stesso concetto 9 :

Prospettiva non è altro che vedere uno sito dirieto uno vetro piano e ben' trasparente, sulla superficie del quale siano segniate tutte le cose che sono da esso vetro indirieto: le quali si possano condurre per piramidi al punto dell'ochio e esse piramidi si tagliano su detto vetro.


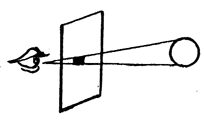
Questa metafora ha una natura già di per se squisitamente geometrica poiché si riferisce a una piramide e alla intersezione di tale piramide con un piano e pone con chiarezza il problema della realizzazione prospettica in termini di proiezione centrale. Tuttavia il processo di riacquisizione di un metodo scientifico, malgrado il chiaro tentativo di emulazione dei classici, non si realizza con facilità come si potrebbe immaginare ed è proprio su queste difficoltà che articoleremo questi interventi. Le difficoltà sono legate a nostra avviso principalmente a due fattori importanti: il contesto storico nel quale tale rinascita avviene (del quale discuteremo in questo articolo) e le difficoltà cognitive che il pensiero incontra nel passare da una logica naturale a una logica formale, trattate nel successivo articolo L'arco di pietre.


Bagliori nel buio.

Il degrado culturale in Europa all'inizio del Medioevo (V, VI, VII dopo Cristo) aveva portato a un livello di analfabetizzazione generale diffusa non solo tra le popolazioni superstiti ma anche nei conventi e nei monasteri dove l'unico ''sapere'' che veniva in un qualche modo tramandato era quello relativo all'attività del culto, come l'armonia musicale o il coputo della data della Pasqua. Gregorio di Tourus nella sua Historia Francorum scritta alla fine del VI secolo osserva sconsolato come la pratica della lettura si fosse estinta nelle città della Gallia. Anche la così detta rinascita carolingia, avviata da Carlo Magno nell'VIII secolo, per quel che riguarda la matematica, è di una povertà sconcertante. Il livello scientifico sembra più basso di quello desumibile dai papiri egizi e ben lontano dalle prime ricerche geometriche della scuola eleatica e pitagorica. Basti pensare che nelle Propositiones ad acuendos juvenes di Alcuino di York 10 , il testo di riferimento per introdurre la geometria e l'algebra nella scuola di Palazzo istituita dallo stesso Carlo Magno, pi greco viene approssimato col numero 4 e si insegna a calcolare l'area di un triangolo isoscele moltiplicando la lunghezza di metà base per quella del lato obliquo, sulla base di fonti forse cinesi o indiane. Mi sembra inutile ricordare in questa sede il calcolo di pi greco di Archimede che fornisce un algoritmo attraverso il quale è possibile calcolare questo numero con una precisione arbitraria eseguendo solo le quattro operazioni dell'aritmetica ed estrazioni di radici quadrate, o la formula di Erone che fornisce l'area di un triangolo in funzione delle lunghezze dei suoi lati.
La riconquista del sapere da parte dell'umanità, avviene attraverso un percorso lungo e difficile, privilegiando gli aspetti più pratici rispetto a quelli teorici, i risultati più che le dimostrazioni spesso mutilate e non capite. Lo stesso metodo assiomatico-deduttivo proprio dell'ellenismo, non viene per lungo tempo compreso e i fondamenti epistemologici vengono trascurati o confinati all'interno della disputa filosofica. I pochi testi greci conservati, di 1000 anni precedenti, sono spesso mutilati, mal commentati e presentano un corpo disorganico e frammentato della scienza antica di difficilissima ricomposizione Gli Elementi di Euclide e l'Almagest di Tolomeo proprio per la loro struttura elementare e sistematica avranno un ruolo importante, ma non sufficiente, in questa difficile ricostruzione che avviene oltre tutto in un contesto politico e culturale completamente diverso.
Lo sviluppo dell'attività commerciale legata agli scambi di merci tra paesi lontani, la formazione delle prime comunità cittadine, delle prime banche, l'introduzione nel XIII secolo della numerazione indo-araba ad opera di Fibonacci, hanno fortemente contribuito a sviluppare un tipo di ''pensiero scientifico'' nuovo ed essenzialmente pratico che trovava nelle scuole d'abaco, sviluppatesi sopratutto nel centro Italia, espressione completa anche sul terreno didattico. Lo stesso Piero della Francesca è autore di un Trattato d'abaco considerato, nel genere, di ottimo livello. Oltre allo sviluppo della nuova numerazione e agli algoritmi di calcolo per le operazioni aritmetiche (compresa l'estrazione della radice quadrata e cubica), questi trattati contenevano una parte di geometria dove si insegnava a calcolare rapporti, aree e volumi.
Questa ''geometria pratica'', come veniva chiamata, cominciava col definire le figure della geometria euclidea e via via venivano esposte varie regole per calcolare le aree e i volumi anche in situazioni complicate come nel caso del calcolo del volume di una botte. Infine, per sottolineare il carattere pratico dell'insegnamento impartito, venivano descritti strumenti di misura agronomica come archipendoli, quadranti geometrici, diottre usate per determinare, ad esempio, l'altezza di torri o di montagne, la larghezza di un fiume, la profondità di un pozzo sfruttando la similitudine di opportuni triangoli. La dove l'autore lo ritenesse opportuno, per giustificare le affermazioni fatte, vi erano rimandi agli Elementi di Euclide testo che appariva del tutto simile a una sorta di indiscutibile scrittura sacra . Mancava insomma qualsiasi riferimento critico alla scelta dei postulati, la cui funzione ed importanza non veniva riconosciuta e sopratutto mancava la consapevolezza di poter tutto ricostruire col solo ausilio del pensiero logico razionale, senza dover fare appello a verità rivelate o metafisiche o a incomprensibili ingarbugliati ragionamenti. Le stesse interpretazioni, semplificazioni e mutilazioni operate nei secoli da copisti e commentatori degli Elementi restituivano nel XIV secolo un'opera confusa nei suoi contenuti metodologici e fondazionali ma straordinaria e divina nella sua capacità di dedurre col solo ragionamento da pochi dati una così copiosa messe di risultati. Divina nel senso etimologico del termine era per Luca Pacioli la sezione aurea, divina nella trattazione neo-platonica ancora presente, l'esistenza di soli 5 corpi regolari, ognuno dei quali dunque, doveva avere un qualche significato filosofico. Significato legato agli elementi fondamentali della natura (aria, acqua, terra, fuoco e quinta essenza) che resterà vivo fino a Keplero come una chiave di interpretazione del mondo che mischia scienza e metafisica, logica umana e creazione divina.

Nello studio della visione, della quale vogliamo occuparci più dettagliatamente in questo intervento, si mischiano in modo naturale diversi piani d'interpretazione: quello fisiologico (legato al funzionamento dell'occhio), quello fisico (legato alla natura della luce) quello filosofico (legato all'ontologia della visione) e quello geometrico che stabilisce come e in quali condizioni oggetti diversi vengono visti uguali. E' chiaro che è quest'ultimo punto quello che più ha a che fare con la rappresentazione pittorica dal momento che il risultato che si desidera ottenere è proprio questa identità tra la visione del quadro e la visione della realtà che il quadro rappresenta. Fatti semplici e legati all'esperienza quotidiana come ad esempio che tra due oggetti uguali quello più lontano si vede più piccolo si traducono immediatamente in una regola di rappresentazione pittorica che impone di disegnare più piccolo l'oggetto più lontano. O anche il fatto che segmenti paralleli che si allontanano in profondità vengono visti non paralleli, come se prolungati dovessero convergere in un punto infinitamente lontano, ha una immediata applicazione alla pittura. Tuttavia questi fatti se restano isolati, non inseriti in una organica trattazione geometrica, non sono sufficienti a dare una rappresentazione realista di un ambiente tridimensionale, non riescono a rappresentare coerentemente la profondità su una superficie piana realizzando il ''miracolo'' di cui parla Alberti.


Analoghe incoerenze illustri

Una della difficoltà nel passare da un approccio empirico basato su esperienze dirette e deduzioni elementari, a un approccio scientifico fondato su oggetti astratti legati tra loro da una teoria generale, consiste senza dubbio nel rendere coerenti tra loro i diversi dati dell'esperienza. Una teoria scientifica è tanto più interessante e valida tanto più riesce a unificare in un solo quadro fenomeni altrimenti slegati e non rapportati tra loro. Il fatto ad esempio che la caduta di un sasso e la rotazione della Luna attorno alla Terra, fenomeni frutto dell'esperienza comune di tutti noi potessero essere pensati come due aspetti particolari di una stessa teoria scientifica è reso possibile solo dalla presenza di una teoria astratta , la meccanica razionale, all'interno della quale è possibile interpretare quelli ed altri fenomeni diversissimi tra loro. E' questo un esempio oggi ben noto e che non desta più stupore e forse per questo, si tende a sottovalutarne il significato epistemologico, penalizzando l'insegnamento astratto, non riconoscendo le difficoltà che si sono dovute superare per costruire questo quadro interpretativo, difficoltà che consistono proprio nell'individuare delle categorie astratte e di manipolarle col pensiero in modo da formare una teoria coerente capace di interpretare e prevedere a un livello più alto la varia fenomenologia. Questo passaggio è tutt'altro che evidente e naturale e riesce difficile anche in situazioni estremamente semplici. Facciamo due esempi assolutamente elementari per evidenziare come non sia così naturale passare da dati empirici locali a un quadro globale coerente.
Il primo esempio riguarda l'uso delle frazioni in Leonardo da Vinci e il secondo il teorema dell'apparente convergenza di raggi paralleli tra loro.

Dice Leonardo 11 :

Lo spatio ch'è infra 'l taglio della bocca e l' principio del naso è la settima parte del volto;[nel disegno è indicato con a b]



lo spatio ch'è dalla bocca al di sotto del mento c d fia la quarta parte del volto; e simile alla larghezza della bocca;[nel disegno si capisce che per bocca si deve anche ora intendere il taglio della bocca]

lo spatio ch'è dal mento al principio di sotto del naso e f fia la terza parte del volto; e simile al naso e alla fronte; [nel disegno è indicato con a b]



 

Queste tre affermazioni, probabilmente frutto di effettive misurazioni, hanno un senso (empirico appunto) isolatamente l'una dall'altra. Leonardo stesso fa tre disegni per rappresentare le sue affermazioni e usa lettere diverse per indicare lo stesso punto (il principio del naso indicato con a nel primo disegno e con e nel terzo, il taglio della bocca indicata con b nel primo disegno e con c nel secondo, il sotto del mento indicato con d nel secondo disegno e con f nel terzo). Questi rapporti tuttavia non hanno una loro interna coerenza, messi insieme porterebbero all'incongrua conclusione che


dal momento che lo spazio tra il mento e il principio del naso (che è un terzo del volto) è la somma dello spazio tra il mento e la bocca (un quarto del volto) con lo spazio tra la bocca e la punta del naso (un settimo del volto). La differenza tra 11/28 e 1|3 non è gran che: essa diventa apprezzabile solo se il volto è abbastanza grande. In questo caso seguendo i rapporti indicati da Leonardo la parte inferiore del volto risulterebbe più grande (esattamente 5|84 più grande) di un terzo dell'intero volto e il profilo non risulterebbe diviso in tre parti uguali come richiederebbe il canone classico riportato da Vitruvio e sostenuto dallo stesso Leonardo.

Il secondo esempio riguarda una tempera dipinta da Pietro Lorenzetti intorno al 1341: un pannello della Beata Umiltà.


I due ambienti di destra e di sinistra, dove sono collocati i personaggi, appaiono presumibilmente come due stanze con muri paralleli e quindi i tre segmenti che abbiamo indicato con 1,2, e 3 rappresentano linee parallele.


E' noto, e l'esperienza empirica ne da una immediata conferma, che due segmenti paralleli, che si estendono in profondità, vengono visti non paralleli cioè come se convergessero verso un determinato punto. E' chiaro allora che si desidera rappresentare su un quadro tale profondità i segmenti andranno disegnati convergenti. Ed è quello che fa Lorenzetti come si vede prolungando i segmenti: i segmenti 1 e 3 si incontrano in un punto e così anche i segmenti 2 e 3.


Tuttavia questi due punti sono nel quadro ben distinti tra loro, mentre un teorema non difficile, ma essenziale nella geometria della visione afferma che due o più segmenti paralleli tra loro, vengono visti convergere a un unico punto. Tale teorema pensiamo fosse implicito nell'Ottica di Euclide dove si afferma, al Teorema 6, che:

Segmenti paralleli, visti da lontano appaiono non paralleli

senza specificare se l'enunciato si riferisca a due, come tutti i commentatori hanno interpretato, o più segmenti paralleli. In realtà la dimostrazione si riferisce al caso di due segmenti, pur restando essenzialmente valida anche nel caso di tre o più segmenti paralleli.


L'Ottica di Euclide e la prospettiva antica

E' nostra convinzione 12 che in tutta l'Ottica , a differenza degli Elementi, si diano, come diremmo oggi, cenni di dimostrazione, cogliendo solo gli aspetti essenziali dei teoremi per dare l'idea di come si debba in generale procedere. Negli enunciati non vengono dettagliatamente specificate le ipotesi che si intende assumere e, nelle dimostrazioni ci si limita spesso a casi particolari descritti in modo sintetico attraverso la figura che illustra il teorema e la sua dimostrazione. Nel testo Le geometrie della visione abbiamo analizzato alcuni teoremi importanti di quest'opera discutendo la struttura delle dimostrazioni, le possibili ipotesi e il massimo livello di generalità nel quale i teoremi euclidei, apparentemente ovvi, mantengono o non mantengono la loro validità. Facendo questo studio ci siamo accorti che, nella maggior parte dei casi, gli enunciati e le dimostrazioni restano valide, con pochissime modifiche, anche in ipotesi molto più generali di quelle indicate dalle figure e riportate nel testo scritto. In particolare la dimostrazione del teorema 6 relativo alla visione di segmenti paralleli, si estende facilmente al caso di tre o più segmenti che vengono sempre visti come se convergessero ad un unico punto. Ora, la conoscenza o meno di questo risultato teorico, non così ovvio sul piano empirico, trova una immediata applicazione nella realizzazione di un dipinto dove i segmenti che rappresentano rette parallele, se prolungati, anche nel quadro debbono vedersi convergere. Il confronto, ad esempio, tra l'ambiente dipinto da Duccio da Buoninsegna nel XIV secolo nella sua Ultima cena e la Stanza delle Maschere, un affresco realizzato nello studiolo di Augusto al Palatino a Roma si pensa nel 30 a.C., mostra quanto cambi il risultato a seconda che si tenga conto o meno del teorema sulla apparente convergenza di raggi paralleli: l'affresco greco-romano, realizzato in una perfetta prospettiva centrale sembra quasi ingrandire le dimensioni anguste dell'ambiente come in un trompe d'oeil, mentre nella pittura di Duccio si ha l'impressione che il tavolo, i cui lati sono presumibilmente paralleli alle pareti della stanza e alle trabeazioni del soffitto, non sia orizzontale e che gli oggetti che contiene debbano come cadere per terra.


Duccio da Buoninsegna: Ultima cena, pannello della Maestà (1308-11)




La stanza delle maschere, al Palatino in Roma (30 a.C)

Non è il caso di riaprire, in questa sede, la secolare polemica se gli antichi conoscessero a meno le leggi della prospettiva o se questa sia invece opera esclusiva dei grandi pittori-scienziati del Rinascimento. In ogni caso crediamo, nel diverso contesto politico culturale, senza solide basi teoriche e con la consapevolezza (forse ingenua) di fare una nuova scienza, vengono alla luce nella seconda metà del XV secolo, ad opera soprattutto di Leon Battista Alberti, Leonardo da Vinci e Piero della Francesca dei testi (e dei dipinti) nei quali le regole della rappresentazione prospettica verngono date esplicitamente e dove si riconosce in modo altrettanto esplicito la necessità di passare da un approccio empirico a uno scientifico. Tra questi testi il De prospectiva pingendi di Piero della Francesca composto intorno al 1485, dopo aver dipinto quei grandi capolavori quali il Polittico della misericordia, La leggenda della vera croce, La flagellazione, è il primo vero trattato dove vengono date in modo disteso e argomentato le regole geometriche alla base della rappresentazione prospettica. L'opera precedente di Leon Battista Alberti, il De pictura, è del 1436. In questo lavoro Alberti, nel divulgare la segretissima scienza, pur rompendo con la tradizione medioevale, fornisce solo un insieme di ricette, senza dimostrazioni, mischiate a considerazioni metafisiche, morali ed estetiche. Le procedure non più custodite segretamente tra le pareti delle varie botteghe d'arte, vengono rese pubbliche ma, come Alberti dichiara esplicitamente, ad uso dei pittori. La centralità della geometria è ampiamente riconosciuta 13:

... niuno pittore potere bene dipignere se non sapea molta geometria.... chi sia ignorante in geometria, né intenderà quelle né alcuna altra ragione di dipignere. Pertanto affermo sia necessario al pittore imprendere geometria.

Alberti, De Pictura, Libro III, n, 53 tuttavia l'opera ha un carattere descrittivo senza un impianto scientifico e tanto meno assiomatico deduttivo. L'intento di Piero della Francesca, il più grande geometra dei suoi tempi come dirà Vasari 14 , è invece quello di comporre, per la prima volta, sull'esempio degli Elementi di Euclide, un trattato geometrico formato da una serie completa di proposizioni, ognuna con una propria dimostrazione, concatenate logicamente tra loro per dar vita alla prospettiva come vera scientia. Piero rappresenta senza dubbio e più di ogni altro quella straordinaria commistione tra arte e matematica che se in Leonardo si diffonde come un nuovo pensiero su ogni frammento della scienza, della tecnica e dell'arte, in Piero diventa consapevole oggetto di studio, fondamento teorico della propria vicenda culturale . Le sue tre opere matematiche, il Trattato d'abaco, il De quinque corporibus regolaribus e il De prospectiva pingendi testimoniano un lavoro intenso ed originale sui vari aspetti della matematica rinascimentale. La cura nel trattare i calcoli algebrici anche molto complicati, la centralità della teoria delle proporzioni come modo di ragionamento, il gusto per le forme poliedriche e per il loro comporsi e decomporsi in altre forme, il tutto filtrato dalla genialità creativa del grande pittore, contribuiscono, crediamo, ad imprimere alla scienza occidentale, che da lì riprende avvio, quel gusto per il bello, per l'armonia che ancora oggi che i cammini si sono così separati, perdura in alcuni scienziati. Tuttavia il tentativo di Piero resta, malgrado le intenzioni, per molti aspetti carente, ancora non completamente svincolato dalla cultura medioevale, con veri e propi errori di ragionamento, con una logica spesso discutibile, senza un chiaro quadro metodologico di tipo assiomatico deduttivo caratteristico della scienza ellenista e del pensiero scientifico in generale, a testimonianza di quanto sia difficile recuperare sino in fondo le basi epistemologiche di un sapere perduto.