|
Il De Prospectiva Pingendi: modello o realtà?
Piero della Francesca è indicato dal Vasari
1
come il miglior geometra che fusse ne' tempi suoi. In effetti la stesura del De Prospectiva
lo distingue nettamente dai matematici medioevali per una caratteristica peculiare: è il primo trattato dell'epoca che si propone di elaborare
una teoria scientifica che dia un valore indiscutibile alla sua applicazione in pittura: dico essere necessaria la prospectiva, la quale discerne
tucte le quantità proportionalmente commo vera scientia
2
La geometria medioevale non aveva affrontato situazioni nuove rispetto alla geometria ellenistica. I contenuti classici erano stati selezionati,
enfatizzati, a seconda dell'epoca, applicati a varie situazioni pratiche, ma senza l'autonomia necessaria alla costruzione di un sistema originale.
L'opera di Piero si pone il fine di costruire una nuova teoria, non quella della visione diretta, già esistente nelle versioni greche e
medioevali dell'ottica, ma quella della rappresentazione prospettica cioè della rappresentazione, su un piano, di oggetti guardati
da un prefissato punto di vista. Le due teorie hanno intenti diversi, ma l'una serve come base all'altra, addirittura la prima contiene, implicite
ma chiare, le indicazioni su cui proseguire per definire la seconda. L'Ottica euclidea, che Piero cita esplicitamente, contiene
teoremi qualitativi che stabiliscono relazioni spaziali o dimensionali tra le apparenze degli oggetti guardati, ma non si occupa,
perché ininfluente per la teoria, di questioni metriche, di misure effettive. La prospettiva rinascimentale si trova di fronte invece
al compito di dare esatte indicazioni grafiche che disegnino le forme volute. La teoria delle proporzioni, permeante di sé la cultura
del '400, ne diventa così lo strumento principale di dimostrazione e di calcolo, mescolando pratici concetti percettivi con classici
elementi geometrici euclidei.
La formazione degli Elementi ha inizio fin dalla scuola pitagorica ed eleatica: l'analisi di proposizioni complesse e significative ha permesso nel
tempo di risalire a proposizioni via via più semplici dalle quali le più ampie dipendevano, fino all'individuazione del gruppo
fondamentale di assiomi. Negli Elementi infine, con un processo di sintesi, dalle semplici proposizioni iniziali individuate si discende a
quelle più complesse attraverso una dimostrazione formalmente corretta.
Piero, per fare vera scientia, avrebbe dovuto necessariamente percorrere una strada analoga: dall'analisi dell'articolata situazione
pittorica del suo tempo e dei metodi che ne permettevano alla fine una corretta esecuzione prospettica, avrebbe dovuto risalire a un corpo
iniziale di assiomi e derivarne deduttivamente i teoremi che ne fornissero sinteticamente le basi. Ma l'impianto assiomatico-deduttivo,
da fondare, anche se sulla falsariga degli Elementi e dell'Ottica euclidea, lo trova a volte impreciso e approssimativo,
persino in errore.
Egli apre la sua opera dichiarandone esplicitamente la natura sensibile
3
:
Puncto è la cui parte non è, secondo i geumetri dicono essere inmaginativo; la linea dicono avere la lunghezza senza
latitudine.
Et perché questi non sono aparenti se non è a l'intellecto et io dico tractare de prospectiva con dimostrazioni le quali
voglio sieno comprese da l'ochio, perhò è necessario dare altra difinitione. Dirò adunqua puncto essere cosa tanto piccolina
quanto è posibile ad ochio comprendere; la line dico essere estensione da un puncto ad un altro, la cui larghezza è de simile
natura che è il puncto. Superficie dico essere larghezza et lunghezza compresa da le linee.
La definizione materiale di punto, già usata da Alberti nel De Pictura, è giustificata dall'esigenza che le cose dette siano comprese
anche dall'occhio, che la loro comprensione astratta sia affiancata da quella visiva.
Questa scelta tra gli enti teorici, quali quelli euclidei di punti e rette, e gli enti fisici da essi rappresentati, anche se debitamente definiti,
costituisce una curiosa necessità per Piero, che fa pensare a una insufficiente assimilazione del metodo assiomatico-deduttivo. Anche la
matematica euclidea nasce esplicitamente come la teoria scientifica dei disegni eseguibili con riga e compasso e i primi tre postulati degli
Elementi, come osserva L. Russo
4
, non sono altro che la chiara trasposizione, a livello teorico, delle operazioni fondamentali eseguibili con
tali strumenti. Ma negli Elementi si trova chiara la volontà di costruire un modello della realtà che si vuol geometrizzare. La scelta
euclidea il sostituire il termine pre-ellenistico ______ (punto) con _______ (segno), potrebbe sottolineare proprio l'intento di
non interrogarsi sulla vera natura del punto, ma di fornirne invece un modello teorico
5
.
Non vi sarebbe in realtà nessuna esigenza di fare la distinzione proposta da Piero. Il fatto che la prospettiva trovi applicazione nel
disegno e l'ottica si occupi invece della visione diretta (che quindi non affronta di fatto rappresentazioni grafiche) non giustifica definizioni
diverse di stessi enti, così come le definizioni e gli assiomi degli Elementi e i teoremi che ne conseguono non hanno necessità di
adeguarsi al fatto che il teorema di Pitagora si applica anche a triangoli concreti, nella vita pratica. In Piero della Francesca invece si
osserva un curioso ribaltamento psicologico: la pratica pittorica non viene vista come approssimazione di una astratta realtà
matematica, ma, viceversa, è il modello matematico da lui costruito che si piega a contaminazioni con la realtà pittorica,
che costituisce nella sua concretezza l'oggetto principale del suo pensiero e dell'opera.
Questo privilegiare intimamente la concretezza della pittura rispetto alla levità della matematica costringe Piero ad aprire il
trattato, appena enunciata la sua prima proposizione, con una precisazione accettabile da un punto di vista empirico, ma non da un punto
di vista rigoroso quale lui vorrebbe proporre. La
prima proposizione del I Libro infatti afferma:
(I,1) Omne quantità se rapresenta socto angolo nell'ochio.
La cosa va da sé da un punto di vista euclideo, osserva Piero, dal momento che il punto non ha estensione, e se si pone l'occhio
(la virtù visiva) in un punto, necessariamente le rette che lo collegano alla grandezza guardata convergono
6
, e quindi formano un
angolo. Ma, continua, la sua definizione empirica prevede un punto con estensione. Questa scelta pone Piero di fronte a un problema: se
il punto ha estensione avrà un diametro non nullo e se la grandezza guardata ha misura minore del diametro del punto, allora non si
forma l' angolo visivo.
Piero affronta il problema specificando che la sua particolare definizione di punto - Dirò adunqua puncto essere una cosa tanto picholina
quanto è posibile ad ochio comprendere - lo rende sì materiale, ma più piccolo di ogni altra cosa visibile
7
, per cui,
ponendo l'occhio nel punto, i raggi visivi necessariamente convergono.
Non si capisce come l'occhio e il punto materiale possano per lui identificarsi allo stesso livello di trattazione (ricordiamo che l'occhio, per
la definizione appena data, vede il punto, per cui è necessariamente minore di esso).
Eppure se smettiamo di leggere come matematici e diventiamo semplici lettori, interlocutori di una conversazione a senso unico con l'autore,
capiamo benissimo cosa questi vuol fare e trasponiamo brutalmente ogni cosa sul piano del disegno, nel quale effettivamente anche l'occhio si
ritrova ad avere la dimensione della punta della matita. Così il rigore logico del modello teorico si scioglie nell'intuitiva e rassicurante
atmosfera dell'ambiente di lavoro, dove a volte il perfettamente uguali e il pressappoco uguali, funzionano nello stesso modo,
riunendosi entrambi in un segno sul foglio o sul quadro, semplificando così molte difficoltà.
L'arco e le pietre
Il De Prospectiva, allora: teoria empirica o teoria scientifica? Russo osserva [...] l'applicazione del metodo scientifico richiede la
capacità di usare contemporaneamente due livelli di discorso (uno interno alla teoria e l'altro riguardante gli oggetti concreti) e di
passare da un livello all'altro con quelle che abbiamo chiamato regole di corrispondenza
8
L'intento dichiarato di Piero è quello di scrivere un trattato di pittura, per artigiani, basato sulla certezza dei fatti matematici e
non sulla pratica empirica o sui metodi di maniera dell'epoca, dei quali si parla nell'articolo L'ombra della cupola. Tuttavia nella sua
stesura incontra qualche difficoltà.
Nelle Città invisibili, di Italo Calvino, Marco Polo descrive a Kublai Kan un ponte, pietra per pietra:
- Ma qual è la pietra che sostiene il ponte? - chiese Kublai Kan.
- Il ponte non è sostenuto da questa o quella pietra - risponde Marco - ma dalla linea dell'arco che esse formano.
Kublai Kan rimase silenzioso, riflettendo. Poi soggiunse:
- Perché mi parli delle pietre? È solo dell'arco che m'importa. Polo risponde:
- Senza pietre non c'è arco.
Sembra che questo sia il dilemma di Piero nell'affrontare l'esposizione del suo trattato di Prospettiva: come parlare dell'arco senza dire delle
pietre? Nella sua opera i due livelli di discorso spesso sono intrecciati, confusi tra loro.
Nella trattazione teorica di argomenti strettamente legati a osservazioni empiriche, a volte esiste la necessità di abbandonare il rigore
espositivo richiesto alle scienze pure per mantenere un contatto cognitivo con le situazioni e le esperienze a cui tali principi si riferiscono,
ma in una mentalità scientifica ben formata questo vincolo non incide sul rigore del metodo. Nei Fenomeni di Euclide, per esempio,
troviamo la sistemazione in forma assiomatico-deduttiva di diciotto teoremi che delineano una semplice teoria astronomica. In questo breve
trattato di astronomia, nel quale sono tra l'altro usati i teoremi dell'Ottica euclidea come strumento deduttivo di proprietà degli
astri, gli assiomi sono presentati in forma discorsiva, mettendo in luce le osservazioni da cui sono stati originati. È indicativo e interessante
leggere a questo proposito le prime frasi dei Fenomeni:
Poiché le stelle fisse sorgono sempre dallo stesso punto e nello stesso punto tramontano e quelle che sorgono insieme, sempre sorgono
insieme e quelle che tramontano insieme, sempre tramontano insieme, e nel moto da oriente a occidente conservano le stesse distanze
reciproche, e poiché ciò capita solo nel caso di cose che si muovono di moto circolare, quando l'occhio sia a uguale distanza
dalla circonferenza in tutte le direzioni, come è dimostrato nell'Ottica, sia posto che le stelle si muovono di moto circolare e che
sono infisse in un unico corpo e che l'occhio dista ugualmente dalle circonferenze dei cerchi
9
.
Gli assiomi qui sono presentati in forma discorsiva ma le spiegazioni iniziali, frutto di una attenta osservazione di ciò che appare,
stabiliscono immediatamente un ponte, una corrispondenza tra gli enti astratti della teoria (punti, cerchi, sfere ecc.) ed entità concrete
delle quali abbiamo consapevolezza attraverso la nostra immersione nel mondo. In questo modo la realtà stessa appare già come
una realtà scientifica, ordinabile all'interno di un sistema formale che, proprio per questo, può avvalersi di risultati
dedotti in altri sistemi formali.
Nel De Prospectiva invece la forma discorsiva è portatrice di una forma di pensiero sociale, quale quello che si sviluppa
nelle conversazioni di tutti i giorni, e porta fuori dall'ambito formale del metodo scientifico. A volte il ragionamento ha una forma
persuasiva, non dimostrativa, a volte si ha ugualmente dimostrazione anche se l'affermazione è indimostrabile. È quanto accade ad esempio
nella seconda proposizione del I Libro
10
:
(I,2) Tucte le base
11
vedute socto uno medessimo angolo, ben che le sieno diversamente poste, s'apresentano a l'ochio equali.
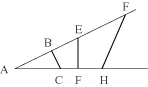
Questo enunciato fa parte di uno degli assiomi dell'Ottica, precisamente il IV: E che le cose viste sotto angoli più grandi appaiano
più grandi, quelle [viste] sotto [angoli] più piccoli più piccole, e uguali quelle viste sotto angoli uguali
12
. Questo assioma definisce il significato geometrico dell'espressione vedere più grande, ...più piccolo..., uguale ma è
faticosamente dimostrato da Piero! Eccone riassunta la dimostrazione, in una mia libera traduzione:
Per esempio, sia in A l'occhio, dal quale partano due linee, AB e AC, e si traccino più basi BC, EF, GH: dico che ciascuna
di queste viene vista dall'occhio A uguale alle altre, e che dall'occhio partono le linee rette e vanno alle basi che si trovano tra dette
linee, e non le intersecano nè le mancano, di modo che l'occhio le prende nello stesso modo. Dico dunque che si vedono uguali
perchè il raggio AC passa per H e per F, in linea retta, e nessuna di quelle basi passa sopra il raggio nè lo manca, e il
raggio AB passa per G e per E, toccandoli, in linea retta, e dunque concluderò ciò che è proposto, cioè che tutte
le basi che sono viste sotto uno stesso angolo sono per l'occhio uguali.
Singolare dimostrazione! Non si definisce cosa vuol dire vedere uguale - la definizione è proprio l'enunciato proposto - ma si
cerca di dimostrare la verità di questa definizione non espressa, di darne alfine una giustificazione. E questo origina
il buffo ragionamento che segue: segmenti sottesi da uno stesso angolo si vedono uguali perchè l'angolo che li sottende,
sottintendendoli, risulta essere proprio il medesimo, nè più grande nè più piccolo di se stesso.
Il ragionare e la logica
Per ragionamento si intende l'insieme dei processi mentali nei quali vengono ricavate delle inferenze, cioè l'insieme dei processi
attraverso cui vengono elaborate nuove conoscenze a partire da conoscenze date. Le conoscenze date sono le premesse, quelle inferite sono le
conclusioni del processo di ragionamento. Quando si parla di razionalità si pensa di parlare di logica
13
, quando si parla di ragionamento
si pensa di essere nell'ambito della razionalità, e ragionamento e logica, in questa sorta di equazione, finiscono per equivalersi
A 30 laureati in matematica o fisica, specializzandi di un corso SSIS
14
, sono state date le seguenti premesse, chiedendo di trarne le debite
conclusioni:
Nessun contabile è un banchiere
Tutti i banchieri sono degli atleti
Il risultato di questo test (perché di un test fai da te si trattava) concorda con quelli ottenuti nelle ricerche svolte in ambito
della psicologia sperimentale
15
, tra studenti universitari di buona intelligenza: la maggioranza ha concluso, erroneamente, che nessun contabile è atleta, qualcuno
ha pensato che non vi fosse alcun risultato valido, nessuno è riuscito a trarre dalle premesse la giusta conclusione
16
:
Alcuni atleti non sono contabili
Molti poi, accettata la giusta conclusione, hanno faticato a convincersi che la conversa alcuni contabili non sono atleti non è valida.
Il tutto, discussioni comprese, ha richiesto come minimo 15 minuti.
Risultati come questo portano spontaneamente al sorgere di domande: è naturalmente logico il nostro pensiero? Si può affermare,
con Piaget, che il ragionamento non è nient'altro che il calcolo proposizionale in quanto tale? Se no, a quali regole si affida allora il
nostro buon senso, nel comune ragionare?
La logica classica, nel senso tecnico del termine, consiste nel dedurre la verità di una proposizione dalla verità di altre proposizioni,
appoggiandosi unicamente sulla loro forma e non sul loro contenuto. Il nostro pensiero comune è sicuramente retto da ben definite regole
inferenziali, ma esse non sono riconducibili interamente a quelle del sistema classico perché sottostanno anche ad altri fattori che non quelli
esclusivamente formali. Nella deduzione naturale sono importanti, ad esempio, i processi pragmatici di comprensione del mondo e di costruzione
continua di significati, che trovano poi risonanza nell'uso del linguaggio e della comunicazione sociale.
Il linguaggio, la comunicazione linguistica e il pensiero inferenziale impegnano capacità cognitive strettamente intrecciate tra loro.
Consideriamo il seguente dialogo:
- Sai se Roberto è tornato?
- Ho visto la sua macchina sotto casa.
La risposta è apparentemente incongrua con la domanda, ma innesca una cascata di deduzioni, immediate, spontanee, così veloci
da non lasciare quasi traccia di sé, che fanno inferire che probabilmente Roberto è tornato. La conversazione si avvale di regole
implicite, non codificate, apprese dagli interlocutori con la pratica, che rende la risposta appropriata Tali inferenze spontanee sono necessarie
per un corretto svolgimento della comunicazione e del ragionamento tra i dialoganti, ma sono assolutamente scorrette da un punto di vista
formale
17
.
Grice
18
ha individuato queste regole conversazionali e ne ha dato una sua classificazione che si può brevemente riassumere in pochi punti:
1) non dire né più né meno di quanto necessario alla conversazione 2) essere pertinenti 3) essere non ambigui, concisi e
non mentire. Pertanto il seguente dialogo:
- Ha un collare per cani?
- No, ma dietro l'angolo trova un negozio di ferramenta.
data la regola n. 2, fa giustamente supporre a chi ha posto la domanda, che nel negozio di ferramenta vendano anche collari per cani.
La forma e la semantica si mescolano nel linguaggio alla conoscenza del mondo e a regole inferenziali economiche, permettendo una veloce
elaborazione del pensiero che guidi comportamenti appropriati alla sopravvivenza. Gli evoluzionisti direbbero che ciò avviene perché
la selezione naturale ci ha plasmato per padroneggiare con prontezza l'ambiente circostante, ed è questo a produrre delle divergenze
tra come ci viene naturale pensare e ciò che è richiesto dall'Accademia. In altre parole, siamo naturalmente strutturati
per una conoscenza non rigorosa, ma sufficientemente approssimata del mondo. Osserva lo psicolinguista S. Pinker
19
La selezione naturale se ne infischia degli ideali dell'educazione progressista, e non ha certo avuto scrupoli a costruire moduli d'inferenza
di utilità immediata che sfruttassero regolarità millenarie ricorrenti nei loro oggetti. [...] il nostro cervello è stato plasmato
per l'adattamento, non per la verità. A volte la verità è adattiva, ma a volte no. I conflitti d'interesse sono insiti nella
condizione umana e noi siamo portati a volere che sia la nostra versione della verità ad avere la meglio, piuttosto che la verità
in sé.
Tutti noi, fin dalla nascita, elaboriamo una sorta di pensiero inferenziale, una qualche forma di scienza intuitiva, che ci guida abbastanza
efficacemente nella vita quotidiana e che ha permesso la sopravvivenza della nostra stirpe - come sottolinea Quine
20
le creature che sbagliano
in modo irriducibile nelle loro induzioni hanno una tendenza patetica ma lodevole a estinguersi prima di riprodurre la loro specie - anche
se ci porta erroneamente a pensare che un numero che ha un grande ritardo
21
al lotto ha più probabilità di uscita degli altri, o che,
verificato che se non gioco non vinco, allora se giocherò vincerò. Ma qual'è il rapporto tra la logica di questo
pensiero naturale e quella formale?
Questa domanda ha per noi particolare interesse. Essa nasce spontanea ogni volta che, come insegnanti, non importa quale sia il livello, ci
sforziamo di educare il pensiero dei nostri allievi al rigore scientifico. Le loro difficoltà hanno una natura molto più complessa
di quel che può pensare, esse, come accenniamo in questo intervento, si trovano anche in menti eccelse come quelle di Leonardo da Vinci o
Piero della Francesca che, nel Rinascimento, più di tutti si è accostato al pensiero scientifico.
La matematica, e in particolare la geometria, è l'ambito nel quale storicamente si è applicata e consolidata la logica aristotelica,
che ha permesso lo svilupparsi del metodo assiomatico-deduttivo. Gli Elementi di Euclide ne sono la testimonianza più conosciuta e la loro
lettura porta la mente a muoversi solo tra i principi e gli enunciati interni al sistema stesso, senza bisogno di altre conoscenze esterne ad esso.
Questa esperienza, inusuale nella vita comune, porta con sé la sensazione di entrare in una dimensione eterea, che fa scrivere a Proclo
22
che studiare quella geometria da teorema a teorema, salendo passo passo verso l'alto, innalza l'anima a un mondo superiore, [...]
le consente [...] di prendere il volo roteando via dalle cose di quaggiù.
Il metodo assiomatico-deduttivo di origine ellenistica, su cui si basa il pensiero scientifico moderno, si è poi perso nei secoli,
per essere recuperato faticosamente a partire dal Rinascimento, indice questo che per concepirlo e applicarlo occorre una notevole sintropia
di pensiero. La storia della matematica e i documenti di cui disponiamo possono fornire indizi rivelatori di quali siano i nodi attorno ai
quali si aggroviglia il pensiero nell'elaborare costruzioni canonicamente razionali. L'analisi che stiamo facendo di alcuni passi dell'opera
di Piero, cercandovi le incongruenze con l'applicazione di un metodo corretto, può aiutare a cogliere le divergenze tra la logica
scientifica e la logica empirica che muove invece il ragionamento naturale. Le difficoltà di Piero sono quelle di tutti noi, connaturate,
tra l'altro, nei limiti di elaborazione dei nostri neuroni e nella naturale costruzione del ragionamento comune sulle regole pragmatiche,
non formali, della comunicazione linguistica.
Il vero per ipotesi
Il ragionare comune si mescola spesso al discorrere, tanto che ancora oggi nell'uso dialettale della lingua, questo termine indica un particolare
modo di parlare-pensare-inferire con un interlocutore. Il discorso comune porta in sé strutture inferenziali che sono pertinenti ed efficaci
nel contesto pragmatico nel quale si svolgono, ma inadeguate su un piano strettamente formale. Il nostro cervello mette insieme capacità e
tecniche per costruire significati nel mondo in cui viviamo e regole che ci consentano di manipolare l'ambiente e di costruire efficaci rapporti
con gli altri. La mente, in questa costruzione sociale, si trova a un crocevia nel quale la cognizione logica e quella emotivo-affettiva
interagiscono su strade promiscue originando regole inferenziali del tutto particolari, in parte in linea con quelle formali, in parte discordanti
o addirittura collidenti con esse. Metodi e algoritmi formali, ottimi per determinare l'incommensurabile o l'esistenza di un pianeta non visibile,
si rivelano antieconomici e inadeguati per inferenze e decisioni pratiche immediate. Le procedure rigorose infatti richiedono tempo e
concentrazione, data la struttura poco capace della nostra memoria di lavoro.
Una regola implicita, quando si è alle prese con la risoluzione di un problema scolastico, è quella di basare il proprio ragionamento
sulle premesse menzionate nella domanda, ignorando ogni conoscenza pratica dell'argomento, ma ciò che succede ragionando con un'altra
persona è esattamente l'opposto. Le persone normalmente concordano nel trovare insensato ignorare ciò che sanno. Lo psicologo
M. Cole e i suoi collaboratori hanno a lungo studiato un popolo liberiano, i Kpelle, dotato di una notevole facilità di parola e portato
al ragionamento e alla discussione. Ecco l'esempio di una incolmabile distanza tra la logica dello sperimentatore e quella dei soggetti
Kpelle, in un test
23
dal quale avrebbero dovuto evidenziarsi le loro capacità inferenziali:
Sperimentatore: Flumo e Yakpalo bevono sempre insieme rum. Flumo sta bevendo rum. Anche Yakpalo sta bevendo rum?
Soggetto: Flumo e Yakpalo bevono rum insieme, ma quella volta che Flumo bevve per primo, Yakpalo non era lì, quel giorno.
Sperimentatore: Ma ti ho detto che Flumo e Yakpalo bevono sempre il rum insieme. Un giorno Flumo beveva rum. Anche Yakpalo quel giorno
beveva rum?
Soggetto: Il giorno in cui Flumo beveva il rum, quel giorno Yakpalo non era lì.
Insomma, lo sperimentatore spesso si sentiva dare risposte del tipo "Yakpalo in questo momento non è qui; perché non andate da lui e
glielo chiedete?" Ce la sentiamo di affermare che i Kpelle sono illogici?
Non se ne voleva assolutamente sapere di accettare per ipotesi che Flumo e Yakpalo bevono sempre insieme rum. In questa logica naturale
un enunciato è vero solo se si è giustificati nell'asserirlo, se ne abbiamo una giustificazione convincente, altrimenti è
rifiutato. Ciò è vero anche nella nostra cultura. L'unica differenza tra i laureati in matematica e gli studenti di un istituto
d'arte
24
sta nel fatto che i primi, educati da studi universitari, accettano senza batter ciglio le premesse e sbagliano il sillogismo, gli altri
cominciano a discutere furiosamente le premesse e non si muovono di lì. Provate a convincere un sedicenne che non ha mai avuto a che fare
con la logica formale che non è idiota assumere come ipotesi che ogni carrozziere è giocatore di scacchi e nessun archeologo è
carrozziere, per veder cosa se ne può dedurre! Comincia subito a protestare
25
che suo zio è carrozziere ma non ha mai giocato a scacchi
in vita sua.
Ma, d'altra parte, se si vuole aggirare il problema dando loro solo premesse sensate:
Ogni animale è un ente che respira
Nessun attaccapanni è un animale
come argomentare che la loro conclusione nessun attaccapanni respira non è giusta? Per loro questa conclusione, è giusta
perché è immediatamente e facilmente inferita e perché è vera, mentre l'inferenza corretta qualche
ente che respira non è un attaccapanni, che richiede un notevole sforzo di pensiero, sembra
imprecisa e generica.
Sembra meno vera, mi è stato detto una volta. Che razza di scienza è quella sillogistica, se ci dà conclusioni
di quel tipo?
Il ragionare comune quindi rende difficile accettare che gli assiomi siano veri per posizione. O sono convincenti, cioè giudicati
realmente veri, o se ne chiede giustificazione. Rende difficile continuare a ragionarci sopra, non si sa più come muoversi. Si
intuisce immediatamente che si stanno cambiando le regole inferenziali, ma non si sa come. Questo vale anche nel momento nel quale si sta
cercando di spiegare il come. La logica dell'insegnante che regge la spiegazione è già irrimediabilmente diversa da
quella dell'alunno che tenta di capire quanto gli viene spiegato. In un incontro con gli studenti di una quarta tecnico-industriale, indirizzo
informatica, avevo proposto il seguente semplice sillogismo condizionale:
Se sono in aereo non sono tranquillo
Sono tranquillo
uno studente mi ha contestato la conclusione non sono in aereo in questo modo E se prima di salire sull'aereo avessi preso un
tranquillante? Sarei tranquillo e sarei in aereo!
La cosa indicativa è che non ha contestato le premesse, ma solo la conclusione, il che significa che considerava vera l'asserzione
che per qualcuno volare sia preoccupante, ma falso che questo fatto influisse in modo irrimediabile sulla tranquillità della persona.
Insomma, dopo aver attribuito un senso alle premesse, criticava la conclusione alla luce delle attività pratiche legate al contesto costruito
sulle premesse stesse.
Si ripropone la situazione del dialogo con i Kpelle, e si intrufola nuovamente l'esigenza di arricchire in qualche modo le proposizioni
presentate, di costruire scenari compatibili con le premesse, senza accettarle solo formalmente, ma immergendole il più possibile nella
vita reale!
La cosa più difficile da far passare nell'insegnamento della logica è proprio l'abbandono della ricerca di un senso, di giustificazioni
opinabili, a favore dell'accettazione di un atteggiamento formale
26
.
Non è difficile quindi tanto l'insegnare l'uso di tavole logiche o di cerchi di Eulero, quanto l'assunzione di un nuovo abito mentale, che
imponga di rimanere entro rigidi binari inferenziali, senza il sostegno di alcuna verità se non quella della correttezza del calcolo logico
che si sta operando, andando contro il comportamento cognitivo usuale.
I solchi della mente
I riferimenti agli assiomi
27
dell'Ottica contenuti nel I Libro del De Prospectiva, non hanno, coerentemente con le esigenze discorsive esposte
nel paragrafo precedente, uno scopo dichiarativo ma esplicativo. Sono inoltre mischiati a risultati di teoremi. Pendiamo ad esempio il seguente
passo del Prologo:
Dunqua dico l'ochio essere la prima parte, perchè gli è quello in cui s'apresentano tucte le cose vedute socto diversi angoli;
cioè quando le cose vedute sono equalmente distante da l'ochio, la cosa magiore s'apresenta socto magiore angolo che la minore, et similmente,
quando le cose sono equali et non sono a l'ochio equalmente distante, la più propinqua s'apresenta socto magiore angolo che non fa la più
remota, per le quali deversità se intende il degradare d'esse cose.
G. Nicco-Fasola, che ha curato un'edizione critica del De Prospectiva, osserva in una nota che in questa parte del suo lavoro Piero
accenna rapidamente a qualcuno dei principi fondamentali posti da Euclide nelle sue supposizioni. In realtà egli sta parlando di
teoremi
28
dell'Ottica, il 5 e il 4 rispettivamente, non di assiomi. Mi sembra di poter affermare che qui Piero, più che tentare di definire
rigorosamente un ambiente che funga da modello, si muove, mentalmente, nel suo contesto naturale di lavoro e richiama semplicemente informazioni
fondamentali, in modo che si possano focalizzare concetti ed euristiche che guidino il pensiero nella comprensione delle conclusioni.
A questo proposito vorrei riprendere la impossibile dimostrazione della seconda proposizione del I° libro, trattata sopra, per rendere
evidenti alcune rappresentazioni mentali inespresse, ma attive, che accompagnano il pensiero di Piero sull'atto visivo. Sembra che egli si
prefiguri che l'occhio percepisca gli oggetti quasi toccandoli con i raggi visivi, e ne valuti le dimensioni solo attraverso l'apertura
dei raggi stessi e che quindi l'inclinazione dell'oggetto rispetto alla bisettrice dell'angolo sia ininfluente per la valutazione stessa. Tali
rappresentazioni facevano naturalmente parte del bagaglio di esperienze dei pittori dell'epoca, abituati a lavorare col prospettografo. Questa
tecnica si attua in vari modi , ma uno molto praticato consisteva nel congiungere con un filo il punto di vista scelto con il punto da proiettare
e di segnare sulla tela o su un supporto idoneo il punto proiettato. Piero stesso, nel terzo libro, userà questo espediente (suggerisce come
filo un crine di coda di cavallo infilato in un ago) per elaborare costruzioni grafiche che mettano in grado di disegnare correttamente oggetti
molto complicati come mazzocchi, capitelli, basi di colonne o addirittura il viso umano.
La dimostrazione impossibile allora, letta con atteggiamento discorsivo, avrebbe potuto risultare sensata e convincente a chi avesse praticato
frequentemente la costruzione di angoli visivi concreti, con ago e filo, e che avesse verificato spesso come i punti esattamente toccati dallo
stesso filo abbiano la medesima proiezione.
L'euristica consiste in una regola o un percorso empirico, più o meno approssimativo, più o meno affidabile, che mettiamo un atto
nel risolvere una certa classe di problemi e che ci viene suggerita dalla pratica con il contesto dei problemi stessi. Nella vita spesso i problemi
si ripetono con regolarità e portano ad elaborare euristiche che, come ruote di carro su un sentiero abitualmente praticato, segnano la mente
con solchi più o meno profondi, nei quali il pensiero scorre spontaneamente, quasi senza sforzo.
Se un problema solitamente affrontato in un contesto pragmatico si pone però in modo astratto, potrebbe non essere riconosciuto
come facente parte di una determinata classe. Il solco allora si perde, il problema stesso diventa difficile da risolvere. Un esempio di
questo stato di fatto ci viene da un esperimento ormai classico - il problema delle quattro carte - ideato dallo psicologo Wason
29
, nel quale
si evidenzia come la forma nel quale si presenta un problema inferenziale sia spesso determinante per la sua soluzione. Wason presentava al
soggetto quattro carte poste su un tavolo, contenenti ciascuna una lettera da un lato e un numero dall'altra. Le loro facce visibili mostravano ,
rispettivamente, una E, un K, un 4 e un 7. Veniva poi data una regola di cui si doveva valutare la validità: "se una carta ha su una faccia
una vocale, allora sull'altra avrà un numero pari" Per verificare se la regola enunciata era vera veniva dato il permesso di girare due carte,
ma solo due.
Il novanta per cento dei soggetti a cui è stato presentato il problema ha voltato correttamente la carta con la vocale, quella con la E,
per verificare che dietro vi fosse un numero pari, ma ha poi continuato in modo errato voltando la carta col numero pari, quella con il 4, compiendo
così un errore di ragionamento
30
. Ma, fatto veramente interessante, se si pone il problema in modo logicamente identico sostituendo il quadro astratto dei numeri e delle
lettere della prima situazione, con eventi usuali del mondo concreto, allora la ruota rientra nel solco e la soluzione corretta si presenta
facilmente, in modo naturale.
Ecco, come esempio, un secondo enunciato del problema equivalente al primo: dobbiamo verificare la
regola "se uno beve birra deve avere almeno diciotto anni". Le carte hanno sulla faccia visibile un bevitore di birra, un bevitore di
Coca-cola, venticinque anni, sedici anni. Quali voltare per verificare la regola? Questa volta la maggior parte delle persone sceglie
giustamente il bevitore di birra e i sedici anni. Eppure i due quesiti sono assolutamente equivalenti, dal punto di vista formale.
Percorsi minimi e verifiche
Data un'opportuna contestualizzazione del problema, la pratica del mondo attiva una serie di rappresentazioni mentali e conseguenti regole
inferenziali legate agli scopi e al raggiungimento di essi, che si mostrano a volte più efficaci di quelle attivate dai soli contesti
formali. Ma non sempre queste strategie risolutive funzionano.
Ecco un esempio di come i nostri giudizi naturali siano basati su euristiche dall'affidabilità incerta e non su procedure rigorose.
Rispondete alla seguente domanda
31
:
Ci sono, in italiano più parole di sette lettere che finiscono in -ndo
(1) - - - - ndo
di quante ce ne siano che hanno una n in terz'ultima posizione?
(2) - - - - n - -
Se la risposta è data in modo intuitivo, molti indicano come più numerose le parole di tipo (1) perché risulta più facile
immaginare parole che finiscono in -ndo che non parole che hanno una n in terz'ultima posizione. Ovviamente questo giudizio è sbagliato
perché tutte le parole di tipo (1) rientrano come casi particolari tra quelle di tipo (2). Come si vede, l'esperienza ripetuta di come stanno
le cose nel mondo spesso ci aiuta a fornircene una rappresentazione mentale giusta, ma a volte ci manda anche completamente fuori strada.
Anche nel ragionamento matematico le euristiche giocano questi ruoli dagli esiti incerti. Nel corso della dimostrazione della proposizione VII
del I Libro, Piero afferma che dati segmenti uguali e angoli che li sottendono, quelli che anno più brievi lati fanno magiore angolo che
quelli che gli anno più lunghi.
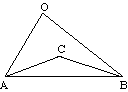
In pratica afferma che dati un segmento AB, due punti C e O e le somme delle loro distanze dagli estremi del segmento, AC + BC, AO + BO, allora tra gli angoli _e Ô che sottendono il segmento è maggiore quello per il quale la somma delle distanze è minore. Questa affermazione di solito convince intuitivamente. Si può pensare che la convinzione dipenda dal fatto che, rappresentandoci il segmento, vediamo che l'angolo massimo è appiattito sul segmento stesso, e in quella posizione, con il punto su AB, la somma delle distanze è minima essendo minimo il percorso tra A e B.
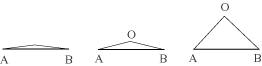
Se poi via via ci alziamo dal segmento, l'angolo ovviamente non può che diminuire e la somma delle distanze aumentare, cosa che ci
porta alla conclusione di Piero. Questa verifica intuitiva è viziata dalla tendenza naturale, alzandosi dal segmento, a stare
al di sopra del segmento stesso, senza valutare quel che succede se il punto si trova in una posizione laterale. Esistono infatti
posizioni di scorcio rispetto al segmento, nel quale l'affermazione di Piero non è valida
32
.
Il campo gestaltico di questo problema facilita l'errore, ma nella vita quotidiana esiste un altro importante fattore che entra in gioco nelle
strategie messe in atto per controllare le credenze o le ipotesi che ci costruiamo riguardo una data situazione: è stata sperimentalmente
rilevata la tendenza a procedere cercando principalmente conferme delle ipotesi considerate
33
attraverso verifiche positive. Vi è inoltre una
certa difficoltà a servirsi di informazioni negative
34
o di strategie basate sulla falsficazione, sulla ricerca cioè di un controesempio. Addirittura il trattare la semplice negazione, non
è facile.
La cosa sembra confermare implicazioni sconfortanti: l'uomo comune è irrazionale, ascientifico, dogmaticamente teso a confermare i propri
pregiudizi invece di affannarsi a cercare controesempi che potrebbero falsificarli. La valutazione si ammorbidisce alquanto se pensiamo che al
di fuori della costruzione di un sistema scientifico, nella vita di tutti i giorni è più adattivo ed economico andare a verificare
induttivamente la sostanza delle proprie ipotesi, anche se così possiamo disporre solo di un sistema di regole locali. Non sono
generalizzabili ma, nella situazione ristretta al nostro particolare ambito di vita, funzionano. Questo atteggiamento dà una conveniente
stabilità alla nostra conoscenza individuale, che trova così un equilibrio tra ciò che è consolidato e la
possibilità di cambiamento, alla quale corrisponde una pari adattiva stabilità della cultura collettiva e delle relazioni
sociali. Ma questa nostra cognizione collettiva convenientemente stabile, se non mantiene in sè gli anticorpi forniti da
una cultura scientifica seriamente difesa e infusa nell'educazione, rischia di assumere forme negative, irrigidendosi in forti dogmatismi
e in sistemi ideologici chiusi e irrazionali, offrendo alla voglia di libertà dell'anima, come uniche vie percorribili, la magia e
l'eversione, artistica o sociale che sia.
La gestione della negazione, dunque, risulta alquanto difficile. Ciò dipende anche dal fatto che a volte negare un attributo ci mette di
fronte a più possibilità. Dire ad esempioquesto oggetto non è rovente non vuol dire che è freddo e non
ci garantisce che possiamo toccarlo senza scottarci. La logica scientifica non ci consente di scegliere a senso un caso particolare
dal cesto dei complementari. La vita concreta invece spesso lo fa, aggirando il problema ma rimettendoci in rigore.
Un uso scorretto della negazione, in questo senso, si trova anche in uno dei teoremi di Piero, il III del I Libro.
(I, 3) Se più base fossero a l'angolo loro oposte orthogonalmente, quella che s'apresenta socto magiore angolo
o ella è magiore o ella è a l'angolo più propinqua.
Nel corso della dimostrazione Piero sta prendendo in esame l'ipotesi che un segmento non sia maggiore di un altro,: Non sia la base BC
maggiore della base EF, per dimostrarne la tesi conseguente dico che BC è più vicino all'angolo A che la base EF
all'angolo D. [...]
Tra le argomentazioni presentate per derivare quanto proposto, troviamo questa affermazione: Dico che HI è uguale a
BC perchè BC è uguale a EF [...]. Ma l'ipotesi diceva che BC non è maggiore di EF, il che comporta la possibilità
che BC sia minore o uguale a EF.
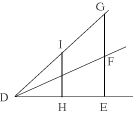
Dalla lettura dell'intera dimostrazione sembra che per Piero la frase o ella è maggiore o è a l'angolo più propinqua
contenuta nell'enunciato del teorema, vada interpretata come segue: o le due basi sono diverse - cosa vera, se una è maggiore
dell'altra - o, se non lo sono - se sono cioè uguali - allora l'una è più vicina al vertice del proprio angolo che non
l'altra. La scelta di Piero è economica, gli consente di non complicare i discorsi moltiplicando le ipotesi e allungando le dimostrazioni
35
,
ma non tiene conto del fatto che se è pur vero che A è maggiore di B ý A è diversa da B, non è altrettando
vero ciò che si ottiene distribuendo la negazione, affermando cioè che se A non è maggiore di B allora A non è
diversa da B, confermando così la naturale difficoltà del pensiero a gestire un percorso attraverso le trappole della negazione.
Il pensiero paralizzato
Supponiamo che A incontri B e abbiano un amico comune, C, che ora lavora in banca. A chiede come vada il nuovo lavoro di C e B
risponde: " Oh, piuttosto bene, mi pare, i colleghi gli piacciono e non è ancora stato arrestato
36
." Come abbiamo ormai più volte avuto occasione di rimarcare, la comprensione di A del significato completo della risposta di B sarà
immediata, ma per noi, che non conosciamo il contesto della situazione, appare chiaro solo che tutto quel che B voleva dire è ben distinto
da quanto ha effettivamente detto.
La produzione di conoscenza ha dei costi, in termini temporali, dovuti alla limitata capacità di memoria che elabora i dati. Formalmente
ogni affermazione vera può dar luogo a infinite asserzioni vere, assemblate col connettivo logico o, così come ogni situazione
di vita può dare origine a un numero molto alto di inferenze, la massima parte delle quali assolutamente inutili per la situazione che si sta
affrontando. Il nostro pensiero non può computare tutte le inferenze possibili
37
scegliendo tra esse quelle pertinenti (e come sarebbe
possibile?) ma si appoggia al contesto in cui si trova e al punto di vista adottato per richiamare dal nostro bagaglio di esperienze le inferenze
appropriate. Nella vita pratica le inferenze producono e guidano le decisioni, e sono guidate da scopi: se oggi piove, uscendo di casa
probabilmente inferiamo che è meglio prendere un ombrello, piuttosto che è certamente vero che oggi piove o la Francia è
un quadrupede. Che senso avrebbe fare una cosa del genere in quella situazione? Parimenti, pur sapendo che possediamo uno stomaco, e che questo
contiene succhi gastrici, quando ci sediamo al volante, il contesto nel quale ci troviamo difficilmente ci porta a concludere che nella nostra
macchina c'è una certa quantità di succhi gastrici.
La contestualizzazione è fondamentale per la possibilità di compiere inferenze, nella vita comune, e quindi di capire, se per capire si
intende l'integrare efficacemente le nuove conoscenze con quelle già presenti nella nostra mente. In questo senso A ha capito immediatamente
B. In questo senso B, per farsi capire da noi, dovrebbe dare informazioni diverse di quelle che ha dato ad A.
L'insegnamento ha il difficile compito di svilupparsi attorno a questa fantastica rete di concetti correlati tra loro che la mente costruisce
raccogliendo continuamente fili sparsi attorno a sé, e deve badare che i nuovi elementi che le mette a disposizione trovino i giusti capi
a cui annodarsi. Nel caso poi che questi giusti fili non ci siano, l'insegnante deve usare pazienza e sensibilità per fermarsi a creare dei
giunti opportuni. L'efficacia dell'azione didattica di un insegnante spesso si infrange proprio contro la sua mancanza di consapevolezza della
difformità tra le proprie logiche e quelle dell'alunno La comunicazione didattica, in questo caso, si incrina
38
.
Il problema del contesto, come abbiamo qui visto in più casi, ogni volta tra loro diversi, si presenta in forme varie e complesse,
facendo apparire la capacità di comprensione singolarmente disomogenea e il ragionamento umano a volte oscuro e contraddittorio.
Queste bizzarrie diventano particolarmente evidenti nelle prove di comprensione di testi scritti. Sui brani scritti vengono ovviamente compiute
molte operazioni cognitive, al di là della semplice decodificazioni delle frasi contenute nel testo. Una serie di esperimenti messi a punto
per indagare sulla comprensione di un brano, risulta essere indicativa sui nostri meccanismi inferenziali. Proviamo a leggere il testo sotto
riportato
39
e a vedere quante idee in esso contenute riusciamo a ricordare:
Se i palloncini scoppiassero, il suono non raggiungerebbe più la sua meta, perché il tutto verrebbe a trovarsi
troppo lontano dal piano giusto. Anche una finestra chiusa impedirebbe al suono di arrivare dove deve arrivare, poiché la maggior
parte degli edifici tende ad essere ben isolata. Dato che l'intera operazione dipende da un flusso continuo di elettricità, se il
cavo si rompesse, questo anche creerebbe dei problemi. Naturalmente l'individuo potrebbe urlare, ma la voce umana non arriva così
lontano. Un ulteriore problema è che una corda dello strumento potrebbe rompersi. Se ciò succedesse non ci sarebbe più
accompagnamento al messaggio. È chiaro che la situazione migliore richiederebbe una minore distanza. Allora ci sarebbero meno problemi potenziali.
Meglio di tutto sarebbe se ci fosse contatto faccia a faccia.
Normalmente se ne ricordano proprio poche. La sensazione di comprensione è bassa e il pensiero è rallentato: non si capiscono parte
delle inferenze presenti nel testo (perché se i palloncini scoppiassero il suono si troverebbe troppo lontano dal piano giusto?....) né
riusciamo a identificare legami logici tra le varie proposizioni (che relazione c'è tra l'urlo di un individuo e lo scoppiare dei palloncini?...).
Ci manca un contesto. Ci mancano cioè delle informazioni che escludano gran parte delle molteplici possibilità di relazione tra
le varie proposizioni del testo, troppe per essere tutte vagliate e confrontate tra loro dal nostro sistema nervoso. Nel caso in questione per
chiarire tutto quanto basta indicare, ad esempio, un
soggetto e uno scopo.
L'indice della comprensione è stato misurato tramite il numero di idee ricordate dopo la lettura, in rapporto al numero totale contenuto
nel brano. I soggetti che hanno letto questo brano lo hanno trovato difficile da capire e la percentuale delle idee rievocate è risultata
molto bassa, solo 3,6 idee su 14.. Fornendo loro un contesto, cioè mostrando il disegno seguente, la rievocazione delle idee migliora
molto, raggiungendo quota 8, ma solo se l'informazione viene data prima della lettura del brano, rimanendo invariata invece se l'informazione
viene data dopo
40
.
Questo risultato conferma come la presenza di un contesto pragmatico attivi automaticamente una rete di conoscenze che lega tra loro gli oggetti
in gioco nella situazione affrontata, permettendo inferenze e la costruzione di relazioni di causalità tra gli elementi del brano. Ciò,
ritengo, viene percepito soggettivamente come comprensione del brano stesso. Se, viceversa, il contesto è formato da oggetti le cui
proprietà sono conosciute solo formalmente, ma non esplorate a fondo pragmaticamente, la capacità di comprensione cala in modo
considerevole.
Gli studenti, e non solo i meno vivaci, di solito si paralizzano mentalmente davanti a un problema di matematica. Smettono di pensare. Non
per indolenza ma per la povertà degli aloni inferenziali che gli oggetti matematici si portano dietro. La semplice
affermazione il triangolo ABC che ha i lati che misurano rispettivamente 3,4,5, e' inscrivibile in una semicirconferenza non
trova spesso comprensione da parte di studenti che pure sanno che i triangoli rettangoli sono iscrivibili in una semicirconferenza. E
ciò non è dovuto al fatto che le informazioni che servono a giustificare l'affermazione sono implicite: anche nel
brano l'uomo al quadro dei comandi stava volando sopra la Normandia vi sono informazioni implicite, ma la comprensione risulta
comunque immediata. Le inferenze che portano dalla presenza di un quadro dei comandi a quella di un aereo risultano molto più
spontanee di quelle che dalle misure dei lati del triangolo portano alla sua forma.
In generale si tende a pensare che i concetti matematici, visto il loro indubbio carattere astratto, non siano inscrivibili in un contesto
più ampio che ne esalti le relazioni con altri concetti, altri settori disciplinari, altre espressioni di pensiero. I concetti matematici
restano punti isolati, procedure formali spesso complicate che conducono a risultati privi di qualsiasi significato concreto e per questo
sostanzialmente incompresi. La tendenza al formalismo che ha trionfato nella didattica della matematica a tutti i livelli negli anni 70 non
ha dato risultati esaltanti. Né è seriamente sostenibile la tendenza opposta, purtroppo sempre più diffusa in questi ultimi
anni, che consiste nell'alleggerire la concettualizzazione matematica riducendo lo studio all'applicazione di una serie di regole o alla blanda
manipolazione di software interattivi che permette verifiche ma anche il dimenticare che occorre infine dimostrare, rinunciando così alla
valenza formativa della materia Non è questa la sede per poter approfondire questo importante tema ma, col pensiero ancora vicino ai nostri
grandi artisti-scienziati del Rinascimento, siamo convinti che sia possibile creare attorno ai concetti matematici opportuni aloni inferenziali
che diano loro spessore e ne permettano una comprensione non solo formale
41
. La storia della matematica è certamente un modo per creare un
contesto vivo, non calato dall'alto, per i concetti anche più astratti, così come possono farlo i legami delle idee matematiche con
quelle della filosofia, della biologia, della fisica, del disegno per fare solo degli esempi.
L'immersione di Piero nel contesto pratico della pittura può essere stata suggerita da intuitive scelte di pensiero e di forme
comunicative con i propri allievi. Il non ripudiare la pratica pittorica ha avuto costi scientifici ma ha reso alla fine più facile
la lettura del complesso trattato che, a parte il difficile e pasticciato
42
inizio - i primi 12 teoremi -, è da considerare un ottimo,
corretto e innovativo testo geometrico. La lettura dell'opera matematica di Piero, che non trascurava gli aspetti anche tecnici e faticosi
del calcolo algebrico, comunica anche a noi oggi quella profonda attrazione per il valore della conoscenza che rendeva l'uomo rinascimentale
orgoglioso nel possederla.
| |




