Scheda didattica Laura Catastini |
||
|
Questo teorema è di grande importanza nella matematica rinascimentale per le numeose applicazioni che trova sia al disegno prospettico che a
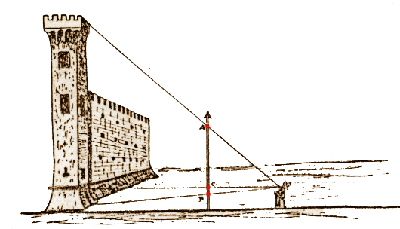
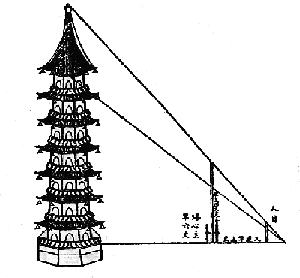
problemi, come vedremo, di natura "tecnologica", certamente presente nella pratica pittorica quando si traguarda sul proprio pennello le dimensioni di
un edificio o di un paesaggio per riportale proporzionalmente sul dipinto. Esso non si trova esplicitamente enunciato negli Elementi di Euclide e forse per
questo Piero lo inserisce tra i
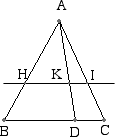
suoi risultati preliminari e ne accenna una dimostrazione. L'enunciato di Piero assume come data una retta BC divisa da un punto D secondo un dato rapporto,
una retta ad essa parallela (equidistante) e un punto A. In queste ipotesi congiungendo B, C, D con A restano individuati sulla parallela i punti H, K, I,
che la dividono nella medesima proporzione
La prova di Piero sembra basarsi su sul teorema 21 del sesto libro degli Elementi che afferma che poligono simili a un terzo sono simili tra loro.
In realtà la dimostrazione è una conseguenza della teoria della similitudine e in particolare del fatto che, se due triangoli sono simili
allora il rapporto tra i lati che comprendono angoli corrispondenti è lo stesso (Elementi, Libro VI, proposizione 4). Poiché infatti le rette sono
parallele i triangoli ABD e AHK hanno gli stessi angoli e anche i traingoli ADC e AKI. Usando in vario modo la proposizione 4 abbiamo HK : BD = AH : AB e quindi
HK : BD = KI : DC da cui, permutando i medi HK : KI = BD : DC Il teorema ha un interessante enunciato inverso che probabilmente era dato per scontato e cioé il fatto che se due segmenti paralleli
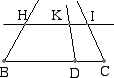
AC e HI sono divisi da un punto D e un punto K secondo la medesima proporzione allora le rette BH, DK e CI convergono verso uno stesso punto.
La dimostrazione si ottiene facilmente considerando il punto A dove si incontrano le rette BK e CI. Tracciando da A la retta AD essa incontra
HI in un punto K'. Si tratta di dimostrare che K'= K infatti in questo caso la retta KD coincide con la retta K'D che per costruzione passa per A. Ma,
ragionando per assurdo, non può essere K diverso da K' perché, per la parte diretta del teroema avremmo HK' : K'I = BD : DC e per ipotesi anche
HK : KI = BD : DC e allora, potendosi in un solo modo dividere un segmento scondo un dato rapporto, K=K'.
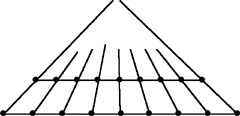
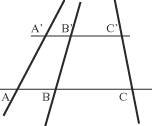
In questa figura i due segmenti sono divisi in 8 parti uguali ciascuno, per questo il rapporto tra i segmenti è uguale al rapporto
tra le singole parti e le rette che congiungono i punti corrispondenti convergono a un unico punto il punto di centrico come sarà chiamato da Alberti.
Il fatto dunque che il fascio di linee parallele che si estendono perpendicolarmente al quadro si rappresentino come linee che convergono a un unico
punto diventa una conseguenza del fatto che la rappresentazione prospettica deve conservare la proporzionalità e la forma di figure poste su piani paralleli al
quadro a diverse distanze.
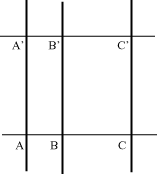
Supponiamo che la linea ABC sia più vicina all'occhio della linea A'B'C'. lI segmento A'C' dunque, essendo più lontano del segmento AC
si vedrà più piccolo e pertanto sul quadro i punti A'C' andranno rappresentati più vicini tra loro. Il disegno sarà quindi del tipo
poiché nella rappresentazione prospettica su un piano i rapporti lungo rette parallele al quadro si mantengono avremmo anche sul quadro,
come nella realtà che rappresentiamo
AB :BC = A'B' : B'C'
e quindi, per il teorema inverso che abbiamo appena dimostrato, le rette AA', BB', CC' devono incontrarsi in un punto.
Questi esempi possono essere didatticamente utili per illustrare con delle interessanti applicazioni la teoria delle proporzioni.
|