Slurm e l'esecuzione parallela di programmi di calcolo Utilizzo "banale" della programmazione parallela per effettuare un'analisi parametrica interessante: l'esempio delle sezioni di Poincaré per il modello di Hénon e Heiles.

1 Framework

1.1 Sezione di Poincaré

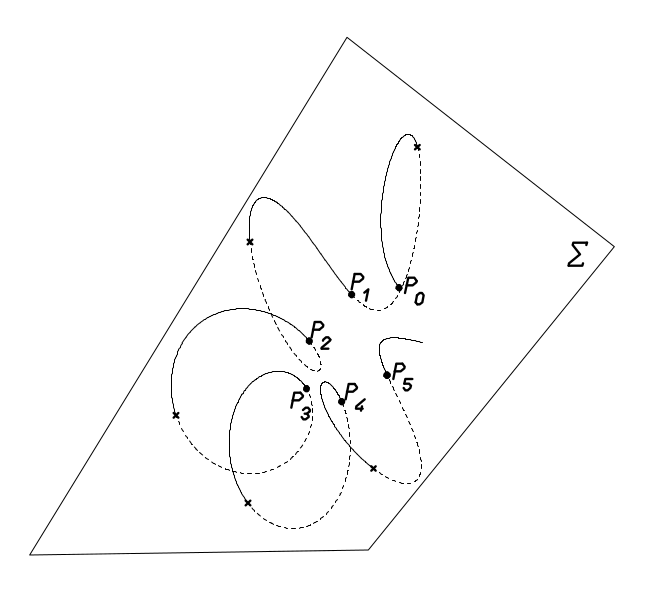
La sezione di Poincaré è un utile metodo per investigare le proprietà di un sistema dinamico. Sia data l’equazione differenziale autonoma in ℝⁿ

e sia Σ ⊂ ℝⁿ una ipersuperficie di dimensione n − 1 ortogonale al flusso Φ _t(x₀) con x₀ ∈ Σ condizione iniziale del sistema. Si definisce sezione di Poincaré l’applicazione

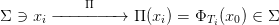
dove T_i è il tempo di ritorno i−esimo del flusso partito da x₀ (e.g. T₁ è il tempo del primo ritorno del flusso su Σ), con la condizione aggiuntiva che il verso della derivata ẋ(T_i) = f(x_i) è di segno concorde con quello iniziale ẋ(0) = f(x₀) rispetto alla normale all’ipersuperficie Σ.

1.2 Modello di Hénon e Heiles

Il modello di Hénon e Heiles è descritto dall’Hamiltoniana

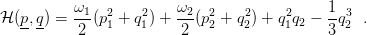
Siamo nel caso n = 4; fissando il valore dell’energia possiamo ottenere delle superfici di dimensione 3, al fine di studiare successivamente le sezioni di Poincaré del modello. Facciamo qualche osservazione sul comportamento di questo modello:

• per valori piccoli dell’energia, ∥q∥ ≪ 1, il sistema si comporta come una coppia di oscillatori armonici con frequenze ω₁ > 0, ω₂ > 0 con una piccola perturbazione costituita dai termini cubici;
• la superficie Σ individuata dall’equazione q₁ = 0 è trasversa al flusso se l’energia è positiva, come segue immediatamente dalle equazioni di Hamilton:

• fissato il valore E dell’energia, le intersezioni del flusso con la superficie Σ giacciono sul sottospazio bidimensionale dato dall’equazione

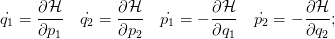
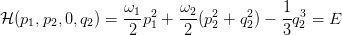
  e deduciamo che un punto (p₂,q₂) delle sezioni di Poincaré individua in modo univoco un’orbita dal momento che abbiamo q₁ = 0 e p₁ dato dall’equazione precedente assumendo che il segno sia positivo;

• il potenziale associato al modello è dato da

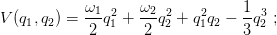
  lo studio di tale potenziale mostra che la sezione di Poincaré è limitata alla regione individuata dall’equazione

  

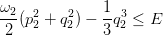
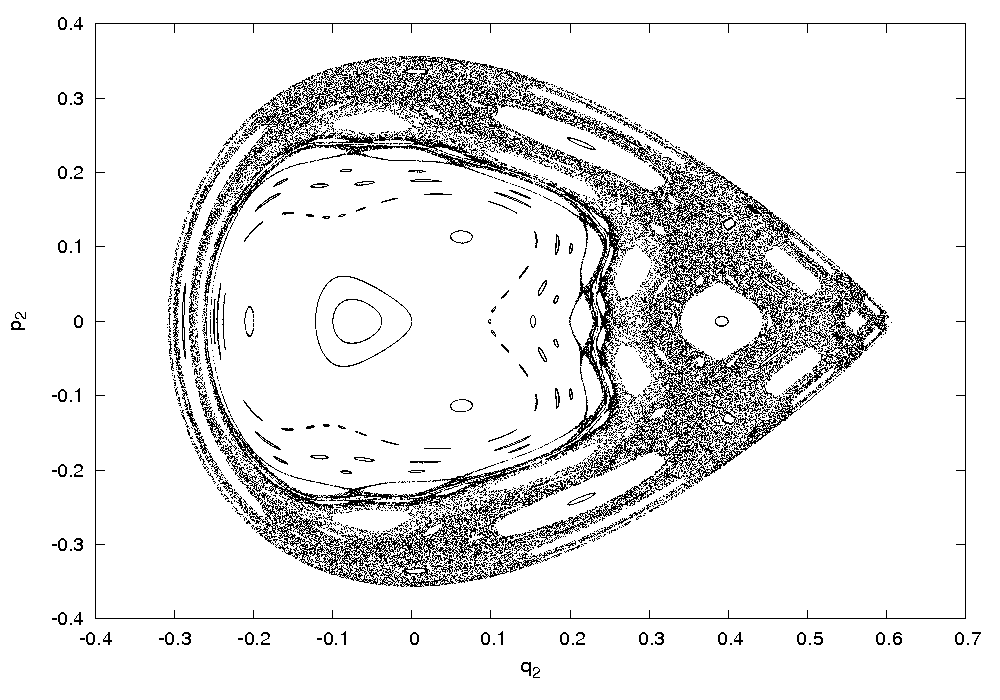
  purchè E sia minore della velocitè di fuga individuata da

  

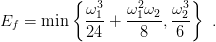
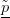• il modello è un sistema reversibile, in quanto autonomo e pari nei momenti: infatti se (p(t),q(t)) è una soluzione, lo è anche la sua coniugata temporale data da ((t), (t)) = (−p(−t),q(−t)).

2 Simulazioni numeriche

Lo studio delle sezioni di Poincaré del modello è stato effettuato utilizzando contemporaneamente 15 core del sistema HPE SuperDome Flex, che è alloggiato nel Centro di Calcolo del Dipartimento di Matematica ed è nominato emmy.

Utilizzando tale infrastruttura, è stato possibile eseguire in parallelo un programma scritto in linguaggio C, che calcola le sezioni di Poincaré per 15 valori diversi delle condizioni iniziali, a fissato livello di energia E = 0.039344. Il suddetto programma e tutti i file che lo mettono in condizione di funzionare correttamente sono inclusi sono stati archiviati e compressi nel file test-slurm-paral.zip. In fase di decompressione, viene creata la cartella test-slurm-paral, al cui interno compare anche il file README.txt, che spiega quali sono i comandi che lanciano l'esecuzione parallela. Si tratta di un esempio che è volutamente semplice. Infatti, il programma che è di gran lunga il più complicato è quello che calcola le sezioni di Poincaré durante l'integrazione numerica del modello di Hénon e Heiles, ma questa parte è quella che deve ovviamente essere sostituita da un codice che si occupa di studiare il problema cui l'utente è interessato.
Si invitano gli utenti di emmy a scaricare il file test-slurm-paral.zip e a creare, localmente sul proprio computer, la cartella test-slurm-paral, per poi leggere il file README.txt. Successivamente, è senz'altro utile copiare tutta la cartella test-slurm-paral nella propria area utente all'interno di emmy e lanciare l'esecuzione parallela dei codici, così come spiegato in README.txt. Queste operazioni, ancorché un po' noiose, dovrebbero permettere una piena comprensione del meccanismo di funzionamento dell'esempio, che dovrebbe essere facilmente adattabile ad esigenze simili nell'ambito delle applicazioni di tipo computazionale cui l'utente è interessato.

L’algoritmo di integrazione utilizzato è il metodo SBAB3C introdotto da Laskar e Robutel in [5]. A sua volta il metodo SBAB3C puè essere visto come una evoluzione di quello del punto centrale, o Leap-Frog, che è accuratamente descritto in [3]. Le seguenti figure mostrano rispettivamente le condizioni iniziali del sistema su cui è stata fatta l’integrazione e le sezioni di Poincaré nello spazio delle fasi (q₂,p₂).

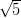Figura 3: Sezione di Poincaré per il caso non risonante (ω₁ = 1 e ω₂ = ( − 1)∕2) del modello di Hénon e Heiles corrispondente al valore dell’energia E = 0.039344 , che è leggermente inferiore a quello di fuga.

3 Conclusioni e ultime annotazioni

Il caso in esame, che è non risonante (cioè tale che ∄(k₁,k₂) ∈ ℤ² \ (0, 0) per cui si ha che k₁ω₁ + k₂ω₂ = 0), mostra una zona centrale con curve chiuse invarianti concentriche. Sono presenti delle zone in cui è possibile il moto ordinato su curve chiuse 1D che stanno intorno ad orbite periodiche. Tuttavia è molto ampia l’area della superficie che viene riempita in maniera apparentemente erratica e abbastanza uniforme dall’orbita che parte da un punto iniziale all’interno di quella stessa regione. Questo comportamento è tipico delle orbite caotiche (cfr. [2]). Lo scenario è quindi il medesimo rispetto a quello descritto, ad esempio, in [6], dove troviamo anche un’analisi per diversi livelli di energia e una breve discussione del caso risonante.

Per quanto riguarda proprio il calcolo parallelo delle sezioni di Poincaré durante l'integrazione numerica del modello di Hénon e Heiles, una breve analisi delle prestazioni di un mini-cluster (che è dedicato ad esigenze puramente didattiche ed è alloggiato in aula 25) è disponibile qui.
In realtà è proprio da quella pagina web, accuratamente preparata dal Dr. Fabio Peluso (laurea magistrale in Matematica conseguita nell'a.a. 2016/17) che è stato ricavato il presente tutorial.

Riferimenti bibliografici