|
A Talete di Mileto (625-547 a.C. circa) si attribuiscono vari teoremi di geometria elementare e i primi tentativi di fornire dimostrazioni razionali.
Dice Proclo:
Talete fu il primo che, andato in Egitto, ne riportò questa dottrina e la introdusse nell'Ellade, e molte scoperte fece egli stesso e di molte dette
lo spunto ai suoi successori affrontando alcuni problemi in modo più generale, altri in modo più pratico.
Sui teoremi attribuiti a Talete gli storici non sono unanimi, non esistono frammenti attribuibili a lui, le fonti che parlano dei suoi contributi
alla matematica sono poche e incerte. Il celebre Teorema di Talete relativo ai rapporti che un fascio di rette parallele individua su una
trasversale pare non fosse noto ai tempi di Talete e neppure la teoria della similitudine che Euclide fa discendere da quel teorema.
Ma di questo ne parleremo più diffusamente nel successivo paragrafo.
Discutiamo ora l'insieme dei teoremi che si ritiene fossero noti ai tempi di Talete riferendoci soprattutto ai Commenti di Proclo che pare
disponesse di una ampia storia della matematica, oggi perduta, scritta da
Eudemo
allievo di Aristotele. Si tratta di una decina
di risultati fondamentali nella geometria piana che formano in un qualche modo un corpo unico di una certa coerenza e compiutezza. Di ogni
teorema riportiamo le testimonianze, i relativi frammenti e qualche commento di natura didattica.
Un diametro divide un cerchio in due parti uguali.
Che invero il cerchio sia diviso in due parti uguali dal diametro l'ha dimostrato per primo - dicono - il famoso Talete.
(Proclo, Commento ...157,10)
Notiamo che questo teorema implica che gli angoli curvilinei formati da un diametro e dalla circonferenza sono tutti uguali a mezzo angolo piatto,
cioè a un angolo retto.
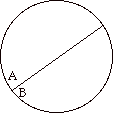
l'angolo curvilineo A è uguale all'angolo curvilino B
Non abbiamo nessun riferimento per capire in cosa potesse consistere la dimostrazione di questo "teorema".
Siamo più propensi a credere che il contributo di Telete possa essere stato quello di avere chiaramente formulato questo enunciato
considerandolo, per altro, del tutto ovvio.
In un triangolo isocele gli angoli alla base sono uguali.
A Talete l'antico, orbene si deve gratitudine sia per molte altre scoperte, sia per il seguente teorema. Si dice appunto, infatti, che per primo
lui abbia riconosciuto ed enunciato - come qualcosa di nuovo - che in ogni triangolo isoscele gli angoli alla base sono uguali, e abbia chiamato
peraltro "simili" - in modo piuttosto arcaico - gli angoli uguali
(Proclo, Commento... 250,20).
Aristotele
(Analitici Primi, I,24, 41b 13-22) riporta una dimostrazione di questa proposizione che lui chiama mediante figure e che utilizza
l'osservazione precedente: la "dimostrazione" si basa sul fatto che una qualunque corda da luogo ad angoli curvilinei uguali
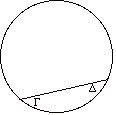
l'angolo curvilineo G è uguale all'angolo
curvilineo D
se ora gli angoli alla base del triangolo isoscele sono rivolti verso il centro abbiamo
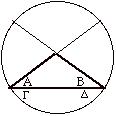
A + G = B + D perché angoli relativi a due diametri
G = D perché angoli relativi a una corda
e quindi sottraendo dagli angoli interi, che sono uguali, angoli uguali, sono uguali i rimanenti A e
B
Osserviamo come in questa dimostrazione alcuni fatti (quelli relativi agli angoli formati dalle corde di un cerchio) non si dimostrano con un ragionamento,
ma si assumono come veri sulla base di una presunta evidenza visiva, mentre viene dedotta, con un ragionamento che fa uso delle
nozioni comuni, che Euclide precisa all'inizio degli
Elementi, una proprietà che a priori non pare
della stessa evidenza. Noi chiamiamo questo tipo di dimostrazione, attribuita da Nicomaco al pitagorico Filolao, "dimostrazione per natura".
Gli angoli opposti al vertice sono uguali.
Questo teorema orbene dimostra che sono uguali gli angoli al vertice formati da due rette che si intersecano: è stato trovato
da Talete per primo secondo quanto afferma Eudemo
(Proclo, Commento ... 259,1. Eudemo di Rodi, frammento 135).
Anche in questo caso abbiamo una dimostrazione "per natura" ampiamente discussa da M. Wertheimer
1.
Guardando la figura vediamo che:
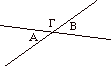
A + G = B + G sono entrambi angoli piatti
e dunque si conclude come prima che A = B.
L'idea di parallelismo è molto antica, legata all'osservazione quotidiana dei raggi di luce o delle goccie di pioggia, e probabilmente
alcune proprietà relative alle rette parallele erano considerate del tutto ovvie. Se, ad esempio, prendiamo un segmento AB e partiamo da A
con un certo angolo a
rispetto ad AB e da B con un certo angolo b allora,
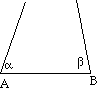
se a+b è minore di
due angoli retti,
le due rette si incontrano e si forma in modo unico un triangolo, cosa che invece non accade se a+b è uguale a
due angoli
retti. Da questo fatto deriva in modo evidente, poichè il triangolo si forma in modo unico, il così detto
secondo criterio di uguaglianza per i triangoli, rigorosamente dimostrato negli
Elementi di Euclide (Libro I, Teorema XXIV)
che Proclo sostiene fosse sicuramente noto a Talete.
Due triangoli che hanno uguali due angoli e il lato compreso sono uguali
La stessa formulazione di Euclide del postulato delle parallele risente di quest'ordine d'idee:
Se una retta venendo a cadere su due rette forma gli angoli interni e dalla stessa parte minori di due retti, le due rette
prolungate illimitatamente verranno ad incontrarsi da quella parte in cui sono gli angoli minori di due retti.
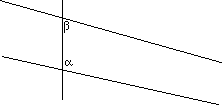
Nella figura abbiamo disegnato verticalmente la retta che "cade". Se a + b
è minore di due
angoli retti, si forma un triangolo, cioè le rette si incontrano, dunque se le rette non si incontrano (né da una parte né dall'altra)
cioè se sono parallele, a + b deve necessariamente dare due angoli retti. Euclide pone questo fatto,
probabilmente considerato ovvio e intuitivamente chiaro dai matematici precedenti, a fondamento della sua geometria, dichiarandone
la validità non come fatto assoluto relativo allo spazio fisico, ma come assunto liberamente scelto e, una volta accettato,
da accettare insieme a tutte le conseguenze che da quello logicamente ne conseguono. In questo possiamo individuare una delle differenze
fondamentali tra un tipo di geometria prescientifica e il modello assiomatico-deduttivo proprio del sistema euclideo e del metodo scientifico
moderno.
Tra le conseguenze di questa proprietà delle parallele ve ne sono alcune ottenibili "per natura" probabilmente note ai tempi di Talete,
sulle quali tuttavia non abbiamo nessuna testimonianza. Ad esempio:
Se due rette sono parallele gli angoli "alterni" sono uguali
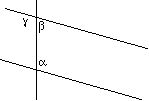
a + b = g + b
infatti, se le due rette sono parallele a + b è uguale a due angoli piatti e, ancora, levando cose uguali
a cose uguali, abbiamo cose uguali, cioè a = g .
Il fatto che, nel caso di due rette parallele tagliate da una trasversale, si formino quaterne di angoli uguali, doveva essere ben chiaro
anche come fatto lampante, da esercitare nei giovani al punto da diventare un automatismo visivo.
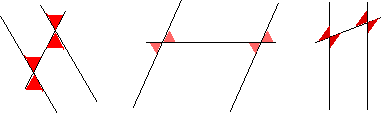
Questa ipotesi è confermata da un passo di Aristotele molto importante (Metafisica Q
9, 1051, 24-33) che altrimenti
risulta di difficile interpretazione. In questo passo Aristotele cerca di descrivere una particolare attività del pensiero
in grado di produrre dimostrazioni "per natura". Riportiamo il passo includendo delle figure che ne esaltano il significato:
Anche le figure collegate alle dimostrazioni geometriche vengono scoperte per mezzo di una attività: le scoprono infatti operando
divisioni [nelle figure assegnate]. Perché un triangolo è due retti?
Perché gli angoli intorno a un punto sono due retti.

A + B + G = due angoli retti?
Se poi fosse stata condotta la retta parallela ad un lato, il perché sarebbe stato chiaro a chi guardava [la figura].

Possiamo dunque considerare noto come conseguenza delle proprietà delle parallele che
La somma degli angoli in un triangolo è un angolo piatto.
Il passo di Aristotele prosegue nel modo segunete:
Perché in generale un angolo in un semicerchio è retto?

A è retto?
Se sono uguali tre segmenti, sia le due basi che la retta apposta dal mezzo, è chiaro anche solo a guardare [la figura] per chi
conosce questo.
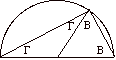
A = B+G e
2G + 2B = due retti.
Così che è chiaro che ciò che è in potenza viene scoperto riportandolo ad una attività: causa ne è che il pensiero è attività...
Osserviamo come questi fatti geometrici anche molto elementari si presentano inizialmente di difficile soluzione mentre un semplice atto creativo
del pensiero, come l'aggiunta di una parallela, o di un raggio, rende la dimostrazione del teorema del tutto palese ed evidente.
Avviene un salto, un "ricentramento cognitivo" attraverso il quale conoscenze pregresse trovano nella nuova situazione che si evidenzia,
una collocazione coerente.
L'attribuzione a Talete del teorema di cui parla Aristotele è confermata da Diogene Laerzio.
Un triangolo inscritto in un cerchio, che abbia come lato un diametro, è rettangolo.
Panfilo [vissuto in età neroniana] dice che Talete, che imparò la geometria dagli Egizi, per primo descrisse un cerchio
attorno a un triangolo rettangolo e che (per questa scoperta) sacrificò un toro. Altri però come Apollodoro il calcolatore,
dicono che fu Pitagora. (Diogene Laerzio, Vite, I, 24-25).
Un altro risultato, simile ai precedenti, che fa uso della "gestalt" degli angoli che una trasversale forma con rette parallele è
la seguente proprietà dei parallelogrammi.
I lati opposti in un parallelogramma sono uguali.

Fatto questo che diventa chiarissimo appena si tracci la diagonale
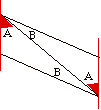
dal momento che questa divide la figura in due triangoli con un lato uguale (la diagonale in comune) e gli angoli uguali
per via delle coppie di rette parallele.
Queste "dimostrazioni" possono essere utili per esercitare un primo approccio alla dimostrazione geometrica e mettono in luce l'aspetto
dinamico e produttivo della dimostrazione. La dimostrazione richiede di intervenire con un atto del pensiero creativo sulla figura
trasformandola in modo da renderne gestalticamente palesi alcune configurazioni che all'inizio erano nascoste. Il tipo di intervento
da fare non è né ovvio né naturale. Le configurazioni che appaiono danno senso alla costruzione perché appaiono contemporaneamente,
l'una in relazione all'altra e non una dopo l'altra. Tracciando la diagonale emergono due triangoli uguali simultaneamente ed è in
questo loro "sorreggersi a vicenda" che la dimostrazione prende forma, anche se, ovviamente, nella descrizione verbale della dimostrazione
si dovrà procedere parlando di un primo triangolo uguale a un secondo triangolo e quindi ecc. ecc.
Scrive M. Wertheimer, Il pensiero produttivo, p. 118:
Il pensiero non procede di necessità, come molti credono, passando semplicemente da un'espressione a un'altra in successione,
formulando proposizioni una dopo l'altra; questo accade qualche volta, ma spesso nel vero atto del pensiero, nei processi genuini,
ciò non avviene. Qui il procedimento va dalle qualità d'insieme osservate, agli elementi visti come parti di un tutto.
|

Talete di Mileto
|